Cosa studia l'insiemistica
Uno dei concetti basilari in Matematica è l’insieme, oggetto principale della branca dell’insiemistica. Si tratta di un raggruppamento di elementi sulla base di una proprietà comune, ma possono essere lettere, numeri o oggetti reali.
Gli insiemi si ritrovano in Algebra, in Aritmetica, in Logica e altri ambiti, per questo sono uno dei primi argomenti che si affronta alle elementari. La loro rappresentazione grafica è molto semplice, così che anche un bambino impara presto a disegnarli.
I diagrammi di Eulero-Venn
Un gruppo o una raccolta di elementi che hanno una caratteristica in comune costituisce un insieme. Ogni oggetto che si classifica al suo interno in linguaggio matematico si dice che gli appartiene.
La concezione dell’appartenenza è fondamentale in insiemistica perché per definire varie categorie di elementi serve capire di quali insiemi facciano parte.
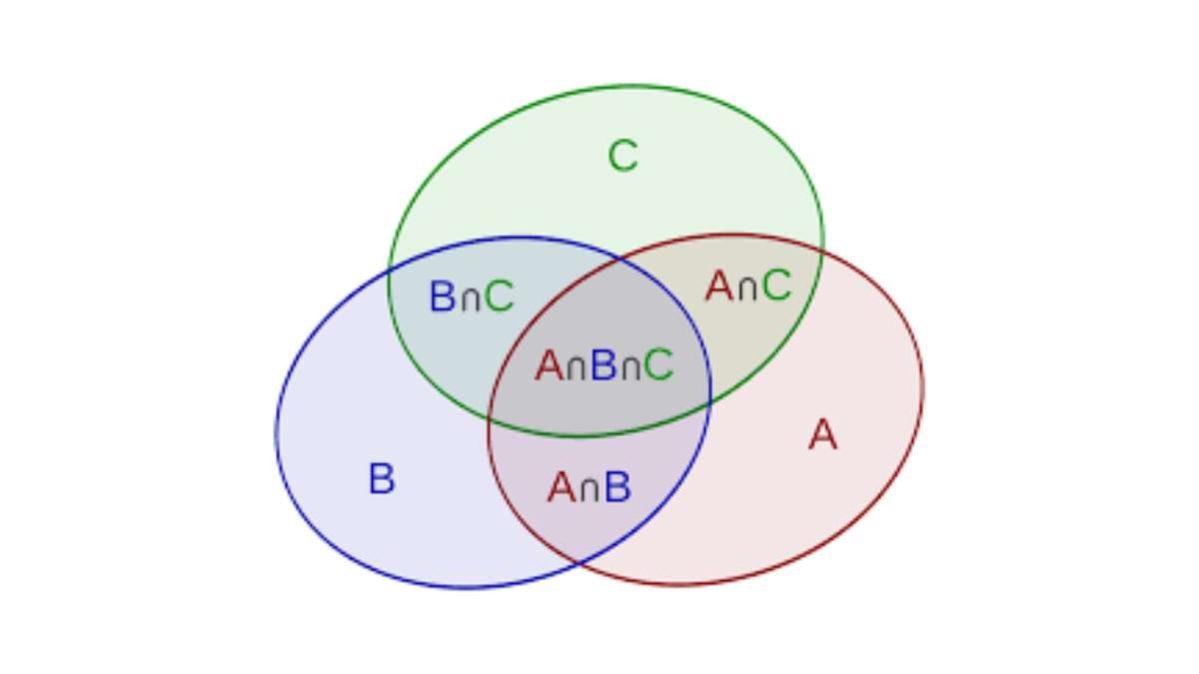
Per rappresentare in maniera grafica gli insiemi si ricorre ai diagrammi di Eulero-Venn, ossia linee chiuse non spezzate ma curve, tanto che la loro forma classica è l’ovale. Dentro il confine rappresentato da questa linea si scrivono o disegnano i concetti o gli oggetti che appartengono all’insieme.
Si tratta di una rappresentazione che aiuta a vedere subito a quale categoria appartiene un elemento ma che risulta poco funzionale quando i gruppi sono numerosi.
Senza dover disegnare diagrammi immensi in insiemistica si può ricorrere allora a un altro sistema alternativo, come l’elencazione o la proprietà caratteristica. La prima di queste prevede di scrivere uno alla volta gli oggetti o i simboli tra due parentesi quadre, separati uno dall’altro da una virgola. Considerando un insieme A per esempio si scriverebbe A = {2, 4, 6, 8}.
La rappresentazione per proprietà caratteristica è anche più semplice perché richiede di descrivere la caratteristica che accomuna gli elementi del gruppo. Per esempio A = {x|x è un numero pari}. Il simbolo di appartenenza è ∈, mentre il suo contrario (non appartiene) è lo stesso simbolo ma barrato, quindi ∉.
L’insiemistica e il concetto di sottoinsieme
Quando si hanno raggruppamenti molto ampi è normale che all’interno di un gruppo non ci sia totale uniformità ma che si possano individuare dei gruppi più piccoli. Possiedono comunque il tratto previsto per far parte dell’insieme principale, ma hanno anche caratteristiche che li fanno spiccare nel mucchio. Ognuno di questi gruppetti costituisce un sottoinsieme, ovvero un insieme che è a sua volta contenuto in un altro.
Portando questo concetto dell’insiemistica agli estremi potremmo dire che ogni elemento se interno a un gruppo può costituire un suo sottoinsieme. Per definirsi tale a livello grafico si deve vedere un diagramma di Eulero-Venn del tutto interno a un altro confine. Non si può parlare di sottoinsieme se c’è una sovrapposizione solo parziale.
Si dice che un sottoinsieme è incluso nel gruppo che lo contiene e il simbolo da usare è ⊂. Scrivere per esempio che A ⊂ B significa che ogni elemento di A appartiene anche a B. Nel caso in cui i due insiemi coincidano perché hanno esattamente gli stessi elementi invece si utilizza il simbolo “=”. Anche in questo caso si tratta di un sottoinsieme vista la definizione, ma se A = B allora A costituisce un sottoinsieme improprio di B.
Le operazione tra insiemi
In insiemistica esistono due operazioni principali, ossia l’unione e l’intersezione. Unire due insiemi significa generare un gruppo più grande che include gli elementi che appartengono a entrambi. Il simbolo dell’unione è la U, quindi per dire che vogliamo unire A e B scriveremo A U B. Se A = {a,b,c,d} e B = {2.3.4} allora A U B = {a,b,c,d,2,3,4}.
L’intersezione invece è un’operazione che mira a individuare gli elementi in comune fra due insiemi. Il simbolo per indicarla è ∩, quindi per definire l’intersezione fra due insiemi C e D scriveremo C ∩ D. Se facciamo un esempio con C = {4,6,8,10,12.14} e D = {4,8,12, 16,20} allora C ∩ D = {4,8,12}. Quando due insiemi non hanno nulla in comune allora la loro intersezione è vuota e possiamo scrivere C ∩ D = {Ø}. Si dice allora che C e D sono disgiunti.
Un’altra operazione frequente in insiemistica è la differenza, che si rappresenta semplicemente con il segno meno fra i due gruppi che consideriamo. Come nella sottrazione classica il risultato è un insieme che contiene gli elementi del primo che non sono comuni al secondo insieme. In pratica rappresentando la loro intersezione con i diagrammi di Eulero-Venn dovremmo togliere la parte in cui si sovrappongono.
L’insiemistica e il prodotto cartesiano
Un’operazione che merita particolare attenzione è il prodotto cartesiano, che si rappresenta con il simbolo “x” fra i due insiemi tra cui si calcola.
Il risultato sono delle coppie ordinate di valori formare da un elemento per ciascun insieme. Per primo però va sempre il primo termine dell’operazione, quindi se facciamo C x D in ogni coppia il primo termine apparterrà all’insieme C.
Per fare un esempio prendiamo C = {1,2,3} e D = {c,f,h} il risultato dell’operazione C x D sarà un elenco di coppie (1;c), (2;f) e così via. Se invece svolgessimo il prodotto cartesiano nella forma D x C le coppie ordinate avranno come primo elemento quello appartenente all’insieme D. Di conseguenza questa operazione di insiemistica non gode della proprietà commutativa.
Nel caso in cui si faccia il prodotto cartesiano fra un insieme qualsiasi e un insieme vuoto vale la stessa regola che c’è per quando si moltiplica un numero per zero. Quindi dato un qualsiasi raggruppamento A e l’insieme vuoto Ø facendo A x Ø otteniamo sempre Ø.
L’insieme universo
Dato che non c’è un grado di specificità dobbiamo ammettere che A può avere più di un insieme universo. Se si tratta di A = {x|x è un mammifero} possiamo avere come U sia l’insieme dei vertebrati che quello di tutti gli animali esistenti.