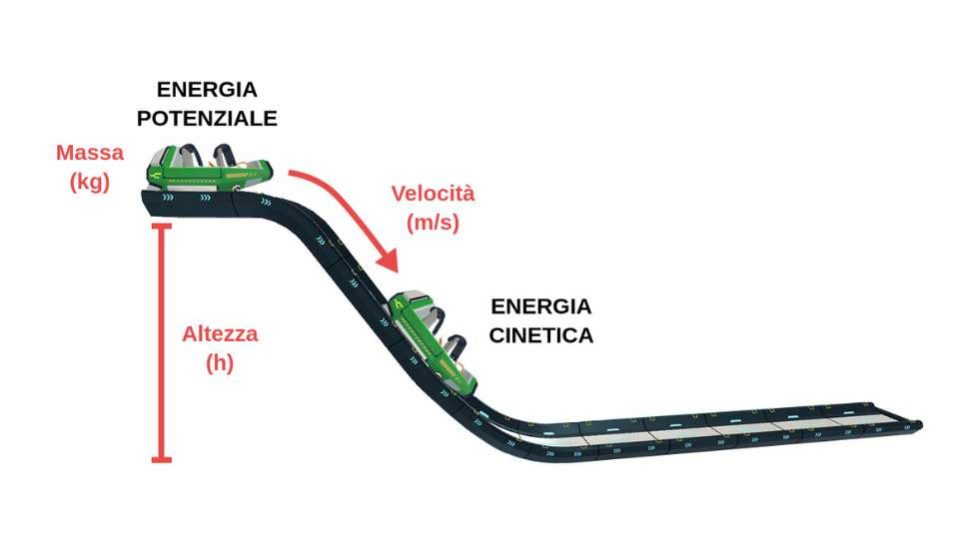
Due forme di energia
Parlare di energia cinetica o potenziale stiamo nominando solo alcune delle possibili forme che l’Energia può assumere. Si tratta però delle due forme con cui abbiamo a che fare più spesso. La prima è quella associata ai corpi in movimento mentre la seconda dipende dalla posizione che ha un corpo rispetto a un campo di forze.
Altre forme che l’energia può assumere sono quella termica (il calore), la forma chimica (per esempio negli alimenti o nel combustibile), o quella elettrica (la corrente).
L’energia cinetica, definizione e unità di misura
Partiamo dalla definizione generale di energia: si tratta della capacità di un corpo di compiere un lavoro. Questa forma particolare però è legata al dinamismo e al movimento. I corpi che la possiedono sono quelli che si muovono nello spazio con un determinato valore di velocità v. Possiamo anche dire che sia l’energia che serve per passare da uno stato di quiete a uno di movimento.
Per indicare l’energia cinetica di solito si ricorre al simbolo K (o Ec in alcuni casi). La sua unità di misura è il joule (J), la stessa che si utilizza per misurare il lavoro e il calore. Il valore di K risulta direttamente proporzionale alla massa del corpo e al quadrato della sua velocità: la formula per calcolarlo infatti è 1/2 mv2.
Di conseguenza l’energia cinetica dipende soprattutto dalla velocità del corpo considerato. Se due auto di massa uguale vanno una a 10 km/h e l’altra a 20 km/h il valore di K della seconda sarà il quadruplo di quello della prima. Per i corpi fermi K è uguale a zero, ma non è possibile avere valori negativi dato che velocità e massa non lo sono mai, a prescindere dalla direzione che segue il corpo.
Energia potenziale: definizione e forme
Mentre l’energia cinetica è associata al moto dei corpi, quella potenziale è quella che possiedono in relazione alla loro posizione, ed è associata alle forze conservative. Possiamo distinguere due varianti di questa forma di energia: quella potenziale gravitazionale e quella elastica.
La prima forma si collega alla forza peso ed è dovuta all’attrazione gravitazionale che la Terra esercita sui corpi. Se abbiamo per esempio un masso in cima a una montagna questo può rotolare giù grazie al suo peso.
Finché è fermo si tratta di energia potenziale, ma se precipita questa si trasforma in movimento. La conversione di questa forma in energia cinetica segue il primo principio della termodinamica, secondo cui l’energia non si crea né si distrugge, ma passa da una forma all’altra.
La forma potenziale elastica invece è quella posseduta dalle molle e dai corpi elastici in generale, che liberano l’energia immagazzinata quando utilizzati.
Le formule per il calcolo l’energia potenziale
Partiamo energia potenziale gravitazionale. Come l’energia cinetica si misura in Joule, ma il suo simbolo è U e la formula per calcolarla è U = mgh. Come prima m rappresenta la massa del corpo, g è l’accelerazione di gravità (9,81 m/s2) e h rappresenta la quota a cui si trova il corpo rispetto a un valore fissato come 0. Questo spesso coincide con il livello del mare.
Il valore di U dunque risulta direttamente proporzionale sia alla massa del corpo considerato sia alla quota a cui si trova posizionato. Per quanto riguarda l’energia potenziale elastica per indicarla si utilizza lo stesso simbolo, ma la formula è diversa dato che si tratta di una forma che riguarda solo le molle. A volte per distinguerle si utilizza il simbolo Ue.
La formula per trovare Ue a prima vista è simile a quella dell’energia cinetica, infatti Ue = 1/2kx2. In questa formula k rappresenta la costante elastica della molla (misurata in N/m) che stiamo considerando, mentre la x è l’allungamento/accorciamento che questa subisce.
Esercizi sull’energia cinetica
Prima di tutto vediamo che tra i dati abbiamo a disposizione la massa (m) e il valore dell’energia cinetica posseduta dal corpo (K). L’incognita è la velocità v, che possiamo trovare facilmente ricavando la formula inversa a partire da K = 1/2 mv2. Per la precisione v = √2K/m, dopodiché basta sostituire i dati e trovare v = √2×6800/550 = 4,9 m/s.
Proviamo ora a calcolare la variazione di K in un corpo che accelera passando da una velocità iniziale (vi) a una finale (vf). Per esempio una moto di massa pari a 120 kg che passa da una velocità di 9 m/s a una di 14 m/s.
Per trovare la variazione basterebbe fare la differenza fra il valore di K1(1/2 mv1) e K2(1/2mv2). Dato che le due formule sono identiche fatta eccezione per il valore della velocità si può scrivere direttamente K1 – K2 = 1/2m(v2 – v1). Perciò 1/2 x 120 x (14 – 9) = 1/2 x 120 x 5 = 300 J.
Esercizi sull’energia potenziale
Dopo l’energia cinetica proviamo ora a vedere un esempio di applicazione rispettivamente della formula dell’energia potenziale gravitazionale e uno per la formula di quella elastica. Partiamo dalla prima, immaginando di avere un masso di 90 kg posizionato in cima a una rampa alta 45 metri. Qual è la sua energia potenziale?
Abbiamo già tutti i dati necessari per svolgere il calcolo, dato che m e h sono note e g è una costante. Così basta sostituire i valori del problema nella formula U = mgh, e quindi il calcolo sarà U = 90 x 9,81 x 45 = 39730 J.
Proviamo adesso a vedere un esempio dove si parla dell’energia potenziale elastica. Abbiamo una molla che subisce un allungamento pari a 0,05 metri e che accumula così Ue = 1,1 J. Qual è il valore della costante elastica della molla?
La formula vista in precedenza era Ue = 1/2kx2 e per trovare k ci serve quindi ricavare la formula inversa. Vale a dire k = 2Ue/x2= 2 x 1,1/0,05 = 44 N/m.