Come individuare una tautologia: pillole per studenti di logica matematica
La logica matematica può sembrare un universo impenetrabile fatto di simboli, connettivi e verità astratte. Ma dietro quella coltre di formalismi si nasconde un modo affascinante di osservare il mondo e ragionare con rigore. Tra i concetti più importanti per chi studia logica c’è la tautologia, un elemento chiave per comprendere la validità dei ragionamenti e la struttura del pensiero logico.
In questo articolo ti accompagneremo passo dopo passo alla scoperta di cosa sia una tautologia, come riconoscerla, e perché sia così centrale nello studio della logica proposizionale.
Una guida pensata non solo per studenti universitari, ma anche per chi è mosso da una curiosità genuina verso la formazione e il pensiero razionale.
Cos’è una tautologia nella logica matematica
Partiamo dalla definizione più classica: una tautologia è una formula logica che risulta sempre vera, indipendentemente dai valori di verità delle proposizioni che la compongono.
Immagina di costruire un’espressione logica con proposizioni semplici, come “P” e “Q”, e connettivi come il “non”, “e”, “o”, “implica”. Se, qualsiasi valore tu assegni a P e Q (vero o falso), l’intera espressione dà come risultato sempre “vero”, allora quella formula è una tautologia.
Qualsiasi sia il valore di P, l’intera espressione è sempre vera. Se P è vero, allora “P” è vero e l’”oppure” regge. Se P è falso, allora “¬P” (non P) è vero, e anche in questo caso l’intera espressione è vera. È il principio del terzo escluso: una proposizione è o vera o falsa, senza vie di mezzo.
Perché è importante riconoscere una tautologia
Nel linguaggio quotidiano, spesso si usano le parole senza badare alla loro struttura logica. Ma nella logica matematica, ogni parola e ogni simbolo hanno un peso preciso. Saper individuare una tautologia non è solo un esercizio tecnico: è un modo per capire se un ragionamento è solido.
In matematica e informatica, ad esempio, le tautologie sono usate per verificare la correttezza di dimostrazioni, circuiti logici e algoritmi. In filosofia del linguaggio, una tautologia può essere la chiave per analizzare le affermazioni prive di contenuto informativo (“Se piove, allora piove”).
Nel contesto della formazione, imparare a riconoscerle affina la capacità di pensiero critico. Capire che una frase è logicamente vera indipendentemente dai fatti può sembrare sterile, ma in realtà è un potente strumento per riconoscere argomentazioni valide e smascherare fallacie logiche.
Le principali strategie per riconoscere una tautologia
A questo punto sorge una domanda naturale: come si fa a capire se una formula è una tautologia? Non sempre è immediato, ma esistono metodi rigorosi che ci vengono in aiuto. I principali sono tre: l’uso della tabella di verità, le leggi della logica e il calcolo proposizionale.
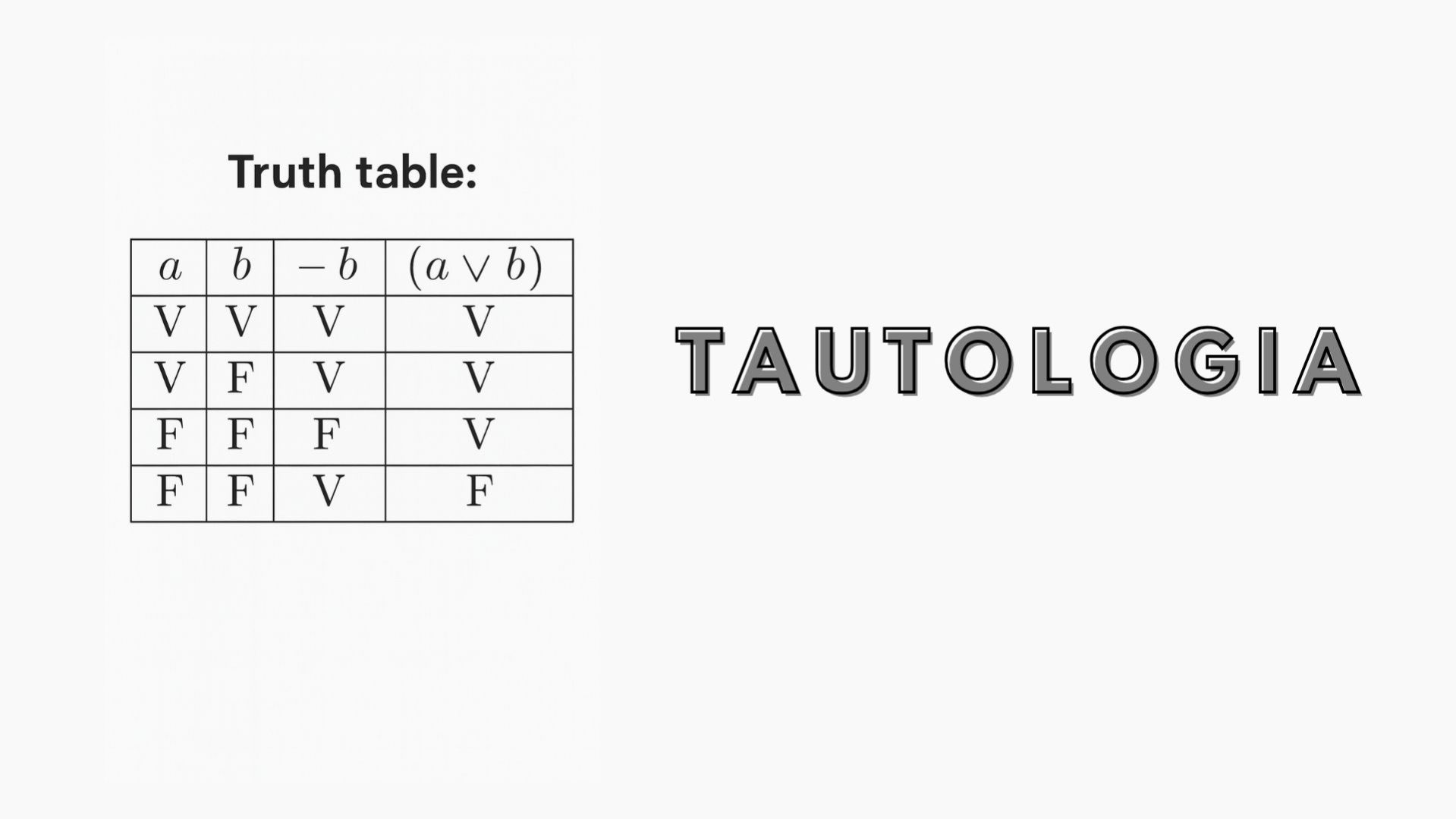
1. La tabella di verità
Il metodo più diretto (e spesso il più didattico) è la costruzione della tabella di verità. Si elencano tutte le combinazioni possibili di verità delle proposizioni componenti e si calcola, riga per riga, il valore dell’intera formula. Se alla fine tutti i risultati sono “vero”, la formula è una tautologia.
2. Le leggi della logica
Con l’esperienza, si impara a riconoscere certe forme logiche che sono sempre vere per definizione. Per esempio, l’equivalenza tra una proposizione e se stessa (“P ↔ P”) è una tautologia.
3. Il calcolo proposizionale
Un approccio più avanzato, ma molto potente, è quello del calcolo proposizionale. Utilizzando regole formali di deduzione, si cerca di dimostrare che la formula può essere derivata senza conoscere i valori di verità delle singole proposizioni. Se è possibile costruire una dimostrazione formale della formula, allora è una tautologia.
Questo metodo è usato frequentemente in matematica, in logica formale e nella verifica dei programmi informatici.
Tautologia, contraddizione e contingente: le tre facce della logica
Per avere un quadro completo, è utile affiancare il concetto di tautologia a quello di contraddizione e contingenza.
-
Una contraddizione è una formula sempre falsa, qualunque siano i valori delle proposizioni.
- Una formula contingente invece può essere vera o falsa a seconda dei valori assegnati. è vera solo quando P e Q sono entrambe vere.
Tautologie nella vita reale: più comuni di quanto pensi
Anche se può sembrare che la tautologia viva solo nei libri di logica, in realtà la incontriamo spesso anche nel linguaggio comune e nella comunicazione.
Frasi come:
-
“Se sarà promosso, allora sarà promosso”
-
“È quello che è”
-
“Ogni numero pari è divisibile per 2”
possono essere viste come forme, più o meno nascoste, di tautologie. Sono affermazioni che, pur sembrando informative, non aggiungono nulla dal punto di vista logico. E proprio per questo, possono essere usate anche per confondere: una tautologia può mascherarsi da verità rivelata, mentre in realtà non dice nulla di nuovo.
Conclusioni: la tautologia come strumento di chiarezza
Imparare a riconoscere una tautologia è un passo importante per chiunque voglia avvicinarsi alla logica matematica con serietà. Non si tratta solo di un esercizio formale, ma di un’abitudine mentale: cercare la verità strutturale dietro le affermazioni.
Che tu sia uno studente alle prime armi o un appassionato di formazione in cerca di strumenti per affinare il pensiero critico, il concetto di tautologia è un alleato potente. Ti aiuta a separare ciò che è logicamente certo da ciò che è opinabile, a leggere tra le righe di un ragionamento, e soprattutto a costruire argomentazioni robuste, impermeabili all’errore.
La logica, in fondo, non è che un modo per guardare con occhi più attenti ciò che già ci circonda. E la tautologia è uno dei suoi strumenti più raffinati.