Come calcolare il volume sfera
Ogni giorno ci misuriamo con strumenti e oggetti di forma sferica: non è quindi strano trovarsi a dover calcolare il volume sfera. La necessità di calcolare il volume di un solido intercorre ogni volta che ci domandiamo quanto materiale interno potrebbe contenere un recipiente. Ogni solido ha la sua formula precisa per il calcolo del volume, e la sfera non fa eccezione.
Questa forma geometrica solida è da molti considerata la più simmetrica: in effetti, su una superficie sferica ogni punto è equidistante dal suo centro. E questo dettaglio è fondamentale per calcolarne il volume. Un calcolo che diventa fondamentale in vari contesti, quali quelli legati alla fisica e all’ingegneria, anche in contesti legati alla vita quotidiana. In questa guida, scopriremo tutte le formule legate alla sfera.
Cos’è una sfera
Prima di analizzare la formula per calcolare il volume sfera, è necessario partire dalle basi e da alcune definizioni preliminari.
Cerchiamo quindi di capire cos’è una sfera, della quale esistono diverse definizioni. Innanzitutto, una sfera fa parte dei solidi. La possiamo definire come quel solido “costituito da tutti i punti che sono a distanza minore o uguale a una distanza fissata r, detta raggio della sfera, da un punto O detto centro della sfera”. Questa è la prima definizione geometrica, riportata anche da Wikipedia.
Ma c’è anche una seconda definizione: la sfera è quel solido che si ricava quando si fa ruotare un semicerchio intorno al suo diametro.
Le parti principali
Dalle definizioni che abbiamo appena analizzato si ricavano le parti principali di questo solido che, come vedremo, serviranno per calcolare il volume sfera.
In primis abbiamo il raggio, termine che indica il segmento che, partendo da un punto qualunque della sfera, arriva al suo centro.
Distinguiamo poi la superficie, ossia tutti i punti che si trovano a una distanza fissa dal suo centro: la parte esterna della sfera, in sostanza. Questa non va confusa con la calotta sferica, ossia una delle due parti in cui una sfera viene divisa da un piano che la taglia. Se il piano passa per il centro, le due calotte sono chiamate emisferi.
Abbiamo poi il settore sferico, ossia la porzione di sfera delimitata dalla superficie di un cono il cui vertice è nel centro della sfera, e dalla superficie di una calotta sferica.
Il fuso sferico, invece, è quella porzione di superficie sferica compresa tra due semicerchi che condividono lo stesso diametro della sfera. Il cosiddetto spicchio sferico, infine, è la porzione di sfera tridimensionale compresa tra due semicerchi che hanno lo stesso diametro.
Volume sfera, la formula base
Ma cosa significa, esattamente, calcolare il volume di una sfera? La definizione di volume, in geometria tridimensionale, è uguale per tutti i solidi. Si tratta della quantità di spazio occupata da un solido.
Per quanto riguarda il volume sfera, la formula per calcolarlo è abbastanza semplice per via delle caratteristiche particolari del solido, che abbiamo analizzato ai paragrafi precedenti.
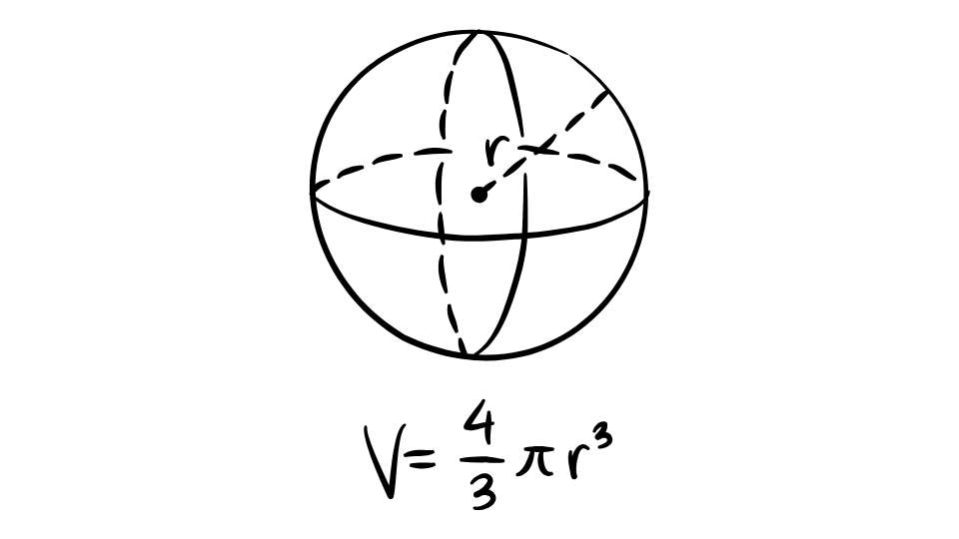
La formula di base è la seguente e deriva dal fatto che la sfera è simmetrica in ogni direzione:
V = 4/3πr3
π è il pi greco, un valore costante approssimato che equivale a circa 3,14. Per quanto riguarda r, invece, è il raggio.
Volume sfera: altre formule utili
Oltre a quella di base per calcolare il volume sfera, esistono anche tante altre formule utili legate a questo particolare solido.
Innanzitutto, quella della circonferenza, che è strettamente legata al raggio e si calcola così:
C = 2πr
Se è nota la circonferenza, al contrario, possiamo calcolare il raggio con la relativa formula inversa:
r = C/2π
Quando è noto il diametro, invece, il raggio si calcola con questa formula:
r = d/2
Questo perché la formula per calcolare il diametro è la seguente:
d = 2r
Se abbiamo a disposizione il dato sul volume sfera, possiamo ricavare il raggio con la seguente formula inversa:
r = 3√(3V/4π)
Quando, invece, abbiamo a disposizione la superficie totale della sfera, calcoleremo il raggio così:
r = √(Stot/4π)
Si tratta della formula inversa per il calcolo della superficie totale, che è la seguente:
Stot = 4πr2
Dato che l’area del cerchio equatoriale è data dalla formula Ae = πr2, la formula inversa con la quale possiamo ricavare il raggio è questa:
r = √(Ae/ π)
Concludiamo l’analisi delle formule legate alla sfera elencando quelle per calcolare le principali parti di questo solido, che abbiamo già elencato ai paragrafi precedenti più in dettaglio, fornendone anche le specifiche definizioni:
- area del cerchio equatoriale: Ae = πr2
- perimetro equatoriale: 2pe = 2πr
- superficie della calotta sferica: S = 2πrh
- volume della calotta sferica: V = πh2 ∙ (r – h/3)
- superficie del settore sferico: S = πr ∙ (r + 2h)
- volume del settore sferico: V = 2/3πr2h
- superficie del fuso sferico: S = (απr2/90°)
- volume dello spicchio sferico: V = (απr3/270°)
Esempi pratici e ambiti di applicazione
La formula del volume sfera e le varie formule inverse possono essere utili nella vita quotidiana. È vero che è difficile (ma non impossibile), trovarsi davanti un recipiente a forma di sfera da riempire. Eppure, ingegneri e fisici possono aver bisogno di calcolare correttamente il volume di una sfera in diverse situazioni.
Inoltre, chi aspira ad accedere ai corsi ad accesso programmato all’Università, dovrà sostenere un test. Spesso, tra i quiz di matematica e geometrica, ci sono anche quelli che richiedono il calcolo del volume interno di un solido.
In questi casi, conoscere la formula per il calcolo del volume sfera è fondamentale.
Ricordiamo, infine, che molti oggetti della vita quotidiana sono sferici. Potrebbe quindi capitare di dover calcolare il volume di una sfera metallica o di una palla, per i motivi più disparati.