Cosa significa condizione necessaria e sufficiente
Trattandosi di un concetto fondamentale della Logica non torna utile solo nella risoluzione dei problemi di Matematica ma in tutti gli ambiti che richiedono di elaborare un ragionamento. Prima però occorre capire cosa significano in forma separata condizione necessaria (CN) e condizione sufficiente (CS).
Si tratta di concetti che in Logica infatti si possono trovare singolarmente, ma se sono presenti insieme si parla di condizione necessaria e sufficiente (CNS). Per comprenderle vedremo degli esempi pratici per tutte e tre le condizioni.
Condizione necessaria e sufficiente: i due presupposti separati
Partiamo a definire che cosa sia una condizione necessaria all’interno di una dimostrazione.
Si tratta di un’ipotesi o presupposto che è essenziale che ci sia perché la tesi che si vuole sostenere risulti valida, infatti senza questa non regge a prescindere. Tuttavia è un presupposto che da solo non basta a dimostrare la tesi.
Per fare un esempio possiamo ricorrere a un caso pratico che si verifica nella vita quotidiana.
Mettiamo che la tesi sia “preparare un piatto di pasta al pomodoro“. In questo caso un esempio di condizione necessaria è “avere a disposizione la pasta“. Non è una condizione necessaria e sufficiente perché dato che non ho nominato il pomodoro non ho già tutti gli ingredienti che mi servono.
Però senza quello fondamentale e necessario è impossibile anche solo iniziare.
La condizione sufficiente invece è un presupposto che permette alla tesi di risultare valida, ma anche se non si verifica non la annulla. Per essere più chiari una stessa tesi può averne di diverse, ed essere comunque verificata.
Un esempio è per la tesi “sono un musicista” scegliere come presupposto “suono il pianoforte.” Questa condizione è di sicuro sufficiente, ma anche se non conosco il pianoforte potrei comunque saper suonare un altro strumento, come la tromba o il flauto.
Ricavare la condizione necessaria e sufficiente
Per farlo prendiamo un argomento di Geometria, ovvero trovare la CNS per definire quadrato una figura geometrica.
Questa frase rappresenta la nostra condizione necessaria e sufficiente.
Che il quadrilatero abbia gli angoli congruenti è necessario, così come vale per i lati. Però da sole non bastano a identificare un quadrato con certezza, e dunque non risultano sufficienti. Insieme però formano un’ipotesi che risulta tale e quale alla definizione del quadrato, quindi una CNS.
Come rappresentare in Logica Matematica la CNS
Se finora abbiamo scritto le ipotesi e le tesi per esteso dobbiamo vedere ora qual è la simbologia corretta per rappresentarle. Ogni enunciato, presupposto o tesi, una volta formulato per non ripetersi si indica con una lettera maiuscola dell’alfabeto.
Questo vale sia che abbiamo una condizione necessaria e sufficiente, sia nei casi in cui ci siano singolarmente quella necessaria o quella sufficiente.
Quindi invece di riscrivere continuamente “ha i lati paralleli” ed “è un parallelogramma” possiamo semplicemente definire la prima proposizione A e la seconda proposizione B. La relazione di implicazione fra A e B si rappresenta tramite una freccia che può essere unidirezionale (=>) o bidirezionale (<=>) a seconda del rapporto che intercorre.
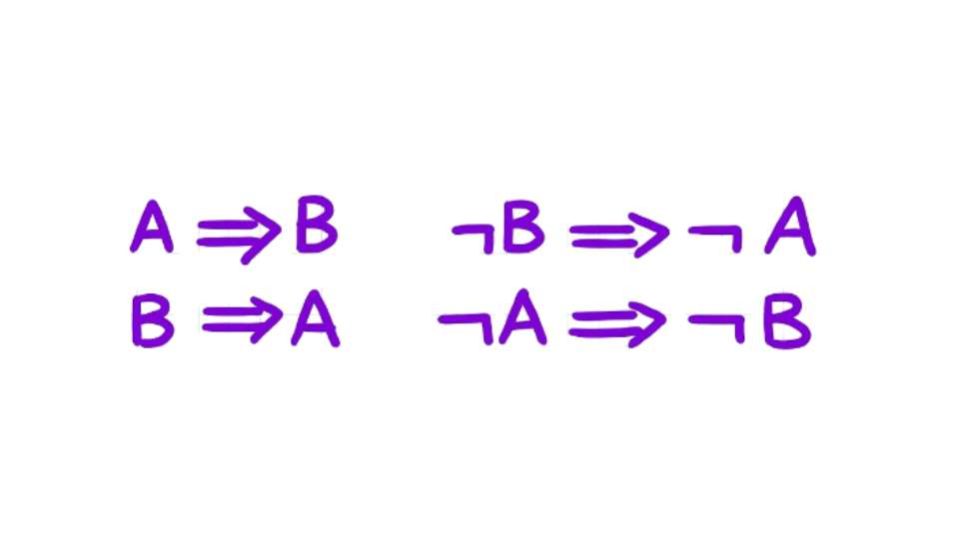
Se A è una condizione necessaria per B scriviamo B => A, ma non A => B. Nel caso in cui invece la proposizione A risulti sufficiente per B la simbologia corretta è A => B, mentre non vale per forza anche B => A. Solo nel caso in cui A rappresenti la condizione necessaria e sufficiente per B possiamo utilizzare la freccia bidirezionale e scrivere A <=> B.
Le regole di inferenza
Quando si ha a che fare con CN, CS e CNS occorre conoscere gli schemi formali su cui basare l’inferenza fra due enunciati. Vale a dire il Modus Ponens e il Modus Tollens, che in logica tornano utili per comprendere la verità o la falsità delle proposizioni considerate.
Nel caso del Modus Ponens se abbiamo un’implicazione fra due proposizioni A => B e sappiamo che la premessa A è vera, possiamo affermare che lo sia anche la conclusione B.
Per esempio nel caso in cui abbiamo gli enunciati A “Paolo è contento” e B “Paolo va a calcetto” vediamo che A è condizione sufficiente per B. Non è però la condizione necessaria e sufficiente, perché sulla base di B non possiamo affermare A.
Per quanto riguarda il Modus Tollens invece ragioniamo nel caso in cui basandoci sempre su due enunciati A e B la conclusione B risulti falsa. In questo caso possiamo affermare che se B => A e ne rappresenta quindi la condizione necessaria allora anche A deve essere falsa.
Esempio di domanda sulla condizione necessaria e sufficiente
Dunque per affermare con certezza che lo sia dovremmo immaginare di precederla con queste parole e capire se il l’affermazione che ne risulta abbia senso.
Prendiamo allora la domanda che segue: “Se e solo se si beve troppo caffè (A) si dorme male di notte (B)“. Considerando vera l’affermazione precedente, quale delle possibili risposte è sicuramente vera?
1. Paola ha dormito male stanotte, quindi ha bevuto troppo caffè.
2. Enrico non ha dormito bene, quindi forse ha bevuto troppo caffè.
3. Se non bevo troppo caffè non mi addormenterò.
Dicendo “se e solo se” ho stabilito che bere troppo caffè è la CNS di “si dorme male“. Prendendo come vera la relazione A <=> B perciò la risposta corretta è la frase 1. La seconda lascia intendere che A sia una condizione sufficiente ma non necessaria, dato che lascia spazio a possibilità diverse per la conclusione. La terza affermazione vede una conclusione diversa, quindi è da escludere.