La dinamica dei fluidi
A volte nei libri si parla di equazione di Bernoulli, più spesso però si trovano le diciture “legge” o “teorema”. In ogni caso ciò che enuncia risulta una relazione fondamentale per la branca della fluidodinamica, ovvero la meccanica dei fluidi in movimento. Per la precisione descrive il moto di un fluido ideale all’interno di una conduttura che anziché uniforme si presenta con sezione e altezza variabili.
Un fluido ideale presenta caratteristiche precise tra cui la mancanza di attrito interno (o meglio, coefficiente di viscosità nullo), densità costante e incomprimibilità (a differenza dei gas). Applicare il teorema ai fluidi reali prevede un’approssimazione che tra i vari aspetti trascura anche le turbolenze interne.
L’equazione di Bernoulli
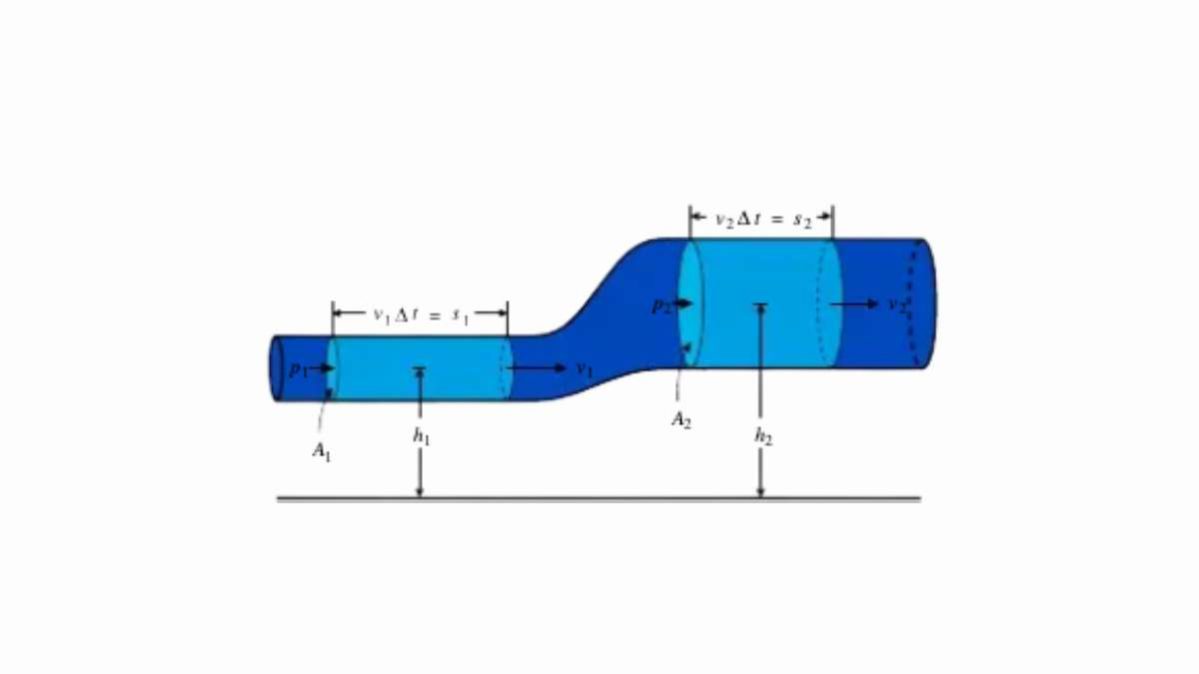
Prima di tutto descriviamo la situazione supposta dal teorema, dove c’è un condotto con sezione e posizione in altezza che cambiano e di cui si considerano due punti distinti.
Indicheremo con S1 e S2 le sezioni, dove S2>S1, e con h1 e h2 le rispettive altezze, sempre con h2>h1. Al suo interno scorre un fluido ideale con velocità v, pressione P (indichiamo con P1 e P2 quella presente a livello delle due sezioni distinte) e densità fissa ρ.
Per descrivere il suo flusso usiamo la formula che segue: P1 + 1/2ρv12 +ρgh1 = P2 + 1/2ρv22 + ρgh2.
Per qualsiasi punto considerato della conduttura dunque abbiamo come costante la somma fra i termini P, 1/2ρv2 e ρgh.
Potremmo dire che l’equazione di Bernoulli è una derivazione del principio di conservazione dell’energia. Se poi abbiamo una conduttura dove la sezione cambia ma non ci sono differenze di quota allora possiamo riscrivere la relazione vista prima in forma più semplice.
Vale a dire che la somma P + 1/2ρv2 risulterà costante per ogni punto del tubo. In sintesi se la velocità cresce la pressione finirà con il diminuire e viceversa.
Un esempio pratico
Dalla sezione del tratto iniziale si passa a una strozzatura dove la pressione scende a 0,25 x 105 Pascal. Qual è la velocità dell’acqua a livello della strozzatura?
P1 + 1/2ρv12 + ρg = P2 + 1/2ρv22 + ρg
Giunti qui possiamo eliminare i due 1 pltre che il fattore g al denominatore semplificandola ulteriormente.
Arriveremo perciò ad avere P1/ρ + v12/2 = P2/ρ + v22/2.
L’incognita presentata dal problema è la velocità che l’acqua avrà una volta giunta alla strozzatura, ovvero v2.
Bisogna perciò ricavare la formula inversa dall’equazione di Bernoulli semplificata, portando v22/2 a sinistra dell’uguale.
Rimane così v22/2 = P1/ρ + v12/2 – P2/ρ, da cui otteniamo v2 = √2/ρ(P1 – P2) + v12. La risposta che si ottiene è circa 13,6 m/s, che mostra come la velocità del fluido aumenti se si restringe la sezione della tubatura.
Applicazioni dell’equazione di Bernoulli
Una delle applicazioni principali di questo teorema la troviamo non tanto nella progettazione delle condutture ma in quella delle ali degli aerei.
Il profilo alare infatti è strutturato in modo che il flusso d’aria scorra con due velocità diverse sulla faccia superiore e quella inferiore.
In particolare questo risulta più veloce sulla faccia superiore, e dunque l’aria esercita una pressione minore. La spinta dal basso invece, ovvero la pressione esercitata sulla faccia inferiore dell’ala, è maggiore: questo consente all’aereo di mantenersi in volo.
La differenza tra le due forze si chiama portanza e contrasta la gravità che spingerebbe il velivolo verso il basso.
I motori dell’aereo di fatto servono a spingerlo in avanti, non a farlo rimanere in quota. Ma la portanza dipende anche da come è inclinata l’ala rispetto alla direzione che prende il volo. Per questo l’angolo varia durante le diverse fasi del volo, in modo che l’aereo sia in grado di spostarsi in orizzontale.
Anche il design delle automobili considera l’equazione di Bernoulli per fare in modo che il mezzo presenti la minor resistenza possibile con l’aria.
In questo modo si evita di sprecare troppo carburante. Troviamo poi delle applicazioni nella progettazione dei sistemi di ventilazione degli edifici oltre che delle turbine idrauliche per produrre energia. Ma conoscere il teorema torna utile anche per prevedere i possibili effetti che delle raffiche di vento quando urtano gli edifici. Il fatto che le case perdano il tetto si spiega proprio grazie alla differenza di velocità e pressione che si genera fra l’interno e l’esterno della casa.
Persino i nebulizzatori di profumo dotati di palloncino per spruzzare la fragranza sfruttano questo teorema. Il liquido finisce con l’essere spinto fuori per la differenza di pressione e velocità dell’aria aspirata.
L’effetto Magnus
In particolare spiega la loro deviazione in un fluido in movimento quando presentano una rotazione (corpi rotanti).
Per sperimentarlo tutto ciò che serve è effettuare un tiro a effetto con un pallone da calcio. Ovvero quando vediamo il pallone descrivere un moto parabolico per poi deviare e tornare indietro. Provocando la rotazione alla palla infatti è possibile riuscire a centrare la porta con un tiro che a prima vista sembra andare fuori.
L’effetto Magnus si utilizza anche nel tennis, in modo da dare alla pallina una traiettoria difficile da prevedere per l’avversario.
Il motivo per cui la palla cambia direzione è legato al fatto che la rotazione provoca un flusso d’aria che non è uniforme a destra e a sinistra dell’oggetto. Senza imprimergli alcuna rotazione invece l’aria scorrerebbe allo stesso modo su entrambi i lati.