La nascita dell'equazione di Nernst
Deve il suo nome al chimico tedesco Walther Hermann Nernst, che si dedicò in particolare allo studio dell’elettrochimica oltre che alla termochimica e alla termodinamica. Per le sue scoperte ricevette il Nobel per la Chimica nel 1920, dopodiché prese a dedicarsi all’Astrofisica.
La sua equazione permette di calcolare il potenziale di riduzione di una coppia redox all’interno di una pila galvanica (es. la pila di Daniell). A Nernst si deve anche una tipologia di lampadina usata nella spettroscopia infrarossa.
Il calcolo del potenziale elettrochimico
Vediamo ora come si presenta l’equazione di Nernst in formula, ricordando che per applicarla dobbiamo trovarci di fronte a una reazione con una specie che si riduce (Red) e una che si ossida (Ox).
Nei libri a troviamo scritta così: E =E0– RT/nF · ln[Red]n/[Ox]m.
Nel dettaglio:
- E è il potenziale elettrochimico che vogliamo calcolare in base alle condizioni in cui si svolge la reazione redox. A destra dell’uguale invece E0 rappresenta il potenziale standard di riduzione, ovvero quello che possiamo misurare a una temperatura di 25°C e una concentrazione delle specie coinvolte di 1 mole per litro (1 M).
- R è la costante fondamentale dei gas perfetti e nell’equazione di Nernst le si assegna il valore 8,314 J/mol·K.
- T corrisponde alla temperatura assoluta della reazione e si misura in gradi Kelvin.
- n è il numero di elettroni che si scambiano la specie ridotta e quella ossidata.
- F è la costante di Faraday, e corrisponde alla carica elettrica contenuta da una mole di elettroni.
- ln è il logaritmo naturale, che ha come base il numero di Nepero e.
- [Red] rappresenta la concentrazione in moli della specie ridotta della reazione redox che consideriamo. L’esponente n rappresenta il suo coefficiente stechiometrico.
- Infine [Ox] è la concentrazione in moli della specie chimica ossidata. Anche qui m è il coefficiente stechiometrico che ha davanti Ox.
L’equazione di Nernst in un caso pratico
In soluzione troviamo gli ioni Cu2+ che si riducono acquisendo due elettroni, secondo la reazione Cu2+ + 2e- = Cu. Dunque ricaviamo che n = 2, conosciamo già E0 e conosciamo anche la temperatura anche se in gradi Celsius. Per trovarla in Kelvin dobbiamo sommare al valore noto 273,15, dunque facciamo 26 + 273,15 = 299,15 K.
Negli esercizi per semplificare il calcolo richiesto dall’equazione di Nernst si sostituisce il logaritmo naturale (ln) con quello decimale (log) moltiplicando il fattore precedente per 2,302 (infatti ln = 2,302 x log). Così possiamo riscrivere la formula nella forma E =E0– 2,302 · RT/nF · log[Red]n/[Ox]m.
Sostituendo i dati a disposizione possiamo ricavare E = 0,345 – 0,029 · log[1]/[0,2], oppure applicando le proprietà dei logaritmi nella forma E = 0,345 – 0,029 · log[1]- log [0,2] .Il risultato finale del calcolo è 0,305 V.
Il caso della pila di Daniell
Al catodo, ovvero al polo positivo, possiamo quindi calcolare il potenziale considerando Cu come Red e Cu2+ come Ox.
Dovremo perciò scrivere l’equazione di Nernst nella forma E(Cu2+/Cu) = E°(Cu2+/Cu) – RT/nF ln [Cu]/[Cu2+].
Invece all’anodo, dove troviamo Zn come Red e Zn2+ come Ox.
In questo caso perciò la formula si può scrivere E(Zn2+/Zn) = E°(Zn2+/Zn) – RT/2F ln [Zn]/[Zn2+].
La pila di Daniel è composta da due recipienti collegati da un ponte salino. Nel primo c’è una lamina di zinco immersa in una soluzione di solfato di zinco (ZnSO4) mentre nel secondo una lamina di rame che affonda in una soluzione di solfato rameico (CuSO4).
La prima si dissocia producendo gli ioni Zn2+, la seconda allo stesso mondo genera gli ioni Cu2+. Il ponte salino invece contiene un elettrolita forte, per la precisione un sale ternario come il solfato di sodio (Na2SO4).
L’equazione di Nernst in chiave fisiologica
Finora abbiamo parlato solo di pile galvaniche e di elettrochimica, ma questa formula si può utilizzare anche per quanto riguarda le reazioni di natura biochimica.
Sappiamo infatti che le cellule del nostro organismo hanno una membrana plasmatica selettivamente permeabile, che consente il passaggio di alcune sostanze.
La permeabilità del plasmalemma a uno ione è legata al potenziale elettrochimico di quest’ultimo in condizioni di equilibrio attraverso questa barriera.
Per la precisione si tratta di un potenziale di equilibrio fra due soluzioni, ovvero l’ambiente extracellulare e il citosol, cioè l’interno della cellula.
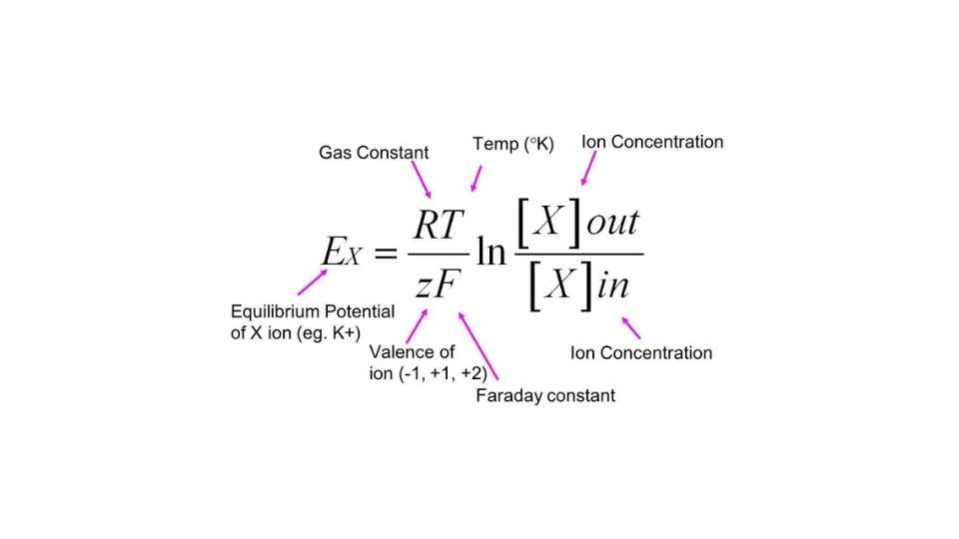
Possiamo scrivere l’equazione di Nernst nella forma µ = µ0 + RT ln[X] + ZN0eV, dove:
- µ e µ0 rappresentano il potenziale dello ioni considerato, nelle condizioni considerate e in quelle standard.
- ln[X] è il logaritmo naturale della concentrazione dello ione.
- Z rappresenta la valenza dello ione.
- N0 è il numero di Avogadro, ovvero la quantità di particelle (atomi o molecole) presenti in una mole di sostanza.
- e indica la carica elementare (del protone o dell’elettrone).
- V infine rappresenta il potenziale elettrico presente in soluzione.