La definizione di equivalenze
La prima cosa da dire su questo argomento è che bisogna stare attenti a non confonderle con le uguaglianze. Queste consistono in due espressioni matematiche separate dal segno uguale, che indica che sono equivalenti in tutte le loro proprietà. Le equivalenze invece sono relazioni di uguaglianza tra due valori espressi con unità di misura diverse, ma che esprimono la stessa quantità.
Possiamo trovare questo tipo di relazione sia con misure espresse sia con le unità fondamentali del Sistema Internazionale (es. metro; litro) che con quelle derivate (es. m/s; N). Per passare da un’unità di misura a un’altra il calcolo da fare si chiama conversione.
Come si affrontano a scuola
Il primo approccio alle equivalenze di solito si fa durante la scuola primaria su tre delle grandezze con cui abbiamo più spesso a che fare nella vita di tutti i giorni. Vale a dire lunghezza, capacità e massa (che però i bambini chiamano peso), che hanno come unità di misura principali il metro(m), il litro (l) e il grammo (g).
Nel calcolo ci si può trovare di fronte a due possibilità: convertire un valore in un’unità di misura inferiore a quella di partenza o viceversa in una superiore. Dopo la conversione avremo la stessa quantità, ma sarà scritta in due modi diversi. Fare equivalenze significa non solo abituarsi a usare più unità di misura ma allenarsi a fare rapidamente calcoli che tornano utili anche nella vita quotidiana.
Prendendo il metro come esempio potremmo dover trasformare una misura in centimetri o in chilometri, mentre per il litro in millilitri o ettolitri. Nel caso della massa partendo sempre da un valore espresso con l’unità fondamentale che è il grammo lo si può trasformare in etto o in milligrammo.
Come approcciarsi alle equivalenze: i prefissi
Restando sulle tre grandezze nominate prima, per capire come effettuare le conversioni dobbiamo capire quali unità di misura si hanno davanti. Per capire quale delle due sia superiore o inferiore tutto sta nel prefisso che hanno: i più comuni sono sei e sono uguali per tutte le unità di misura.
Prendiamo la lunghezza: il metro è l’unità di riferimento da cui ricavare multipli e sottomultipli. I primi tre multipli in ordine crescente sono il decametro/dam (equivale a 10 metri), l’ettometro/hm (100 metri) e il chilometro/km (ovvero 1.000 metri). Quindi deca-, etto- e chilo- indicano rispettivamentr x10, x100 e x1.000.
Vediamo ora i sottomultipli più comuni nel calcolo delle equivalenze. Andando dal più grande al più piccolo i primi tre sono il decimetro/dm (0,1 metri), il centimetro/cm (che equivale a 0,01 metri) e il millimetro/mm (un millesimo di metro). Quindi deci-, centi- e milli- richiedono di dividere l’unità principale, ovvero il metro, rispettivamente di 10, 100 e 1.000 volte.
Questi sono i principali, ma in alcuni contesti possiamo trovarci a dover operare con sottomultipli o multipli di gran lunga inferiore/superiori. Per esempio il Megametro/Mm (1 milione di metri) o il micrometro/µm (0,000001 m, quindi un milionesimo).
Affrontare gli esercizi
Per fare un esempio un esercizio può chiedere di convertire 200 mg (milligrammi) in dg (decigrammi). La seconda grandezza è superiore di 100 volte, quindi dovrò dividere per 100 il valore di partenza. Il calcolo perciò è 200/100 = 2 dg.
Viceversa, se abbiamo la misura di partenza pari a 0,8 ettolitri (0,8 hl) e vogliamo sapere a quanti litri corrisponde dovremo moltiplicare, perché i litri sono un’unità di misura inferiore. Faremo perciò 0,8 x 100 = 80 litri (l).
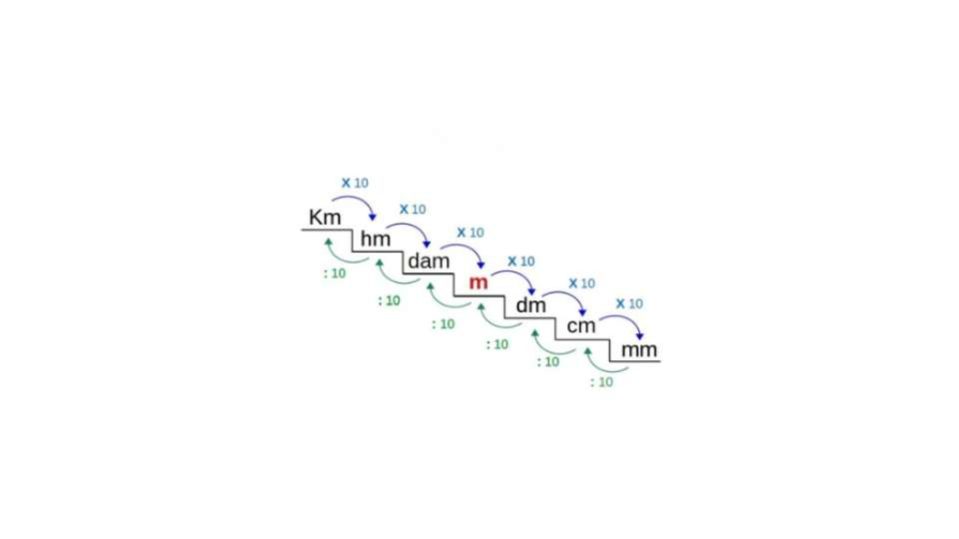
Per fare rapidamente le conversioni richieste dalle equivalenze la cosa migliore è rappresentarle come dei passi su una scala. Questa si può disegnare patendo dal centro di un foglio, con il primo gradino che corrisponde all’unità fondamentale e poi procedendo con gradini che scendono e altri che salgono.
Ogni “gradino” corrisponde a una variazione di dieci volte rispetto all’unità di misura presente sul gradino precedente. Andando verso l’alto si moltiplica il valore, mentre se si scende lo si divide. Quindi se una conversione richiede di salire di due gradini verso l’alto bisognerà moltiplicare il valore per 100. Se invece serve scendere di tre gradini il calcolo da fare è una divisione per il fattore 1.000.
Alcuni casi particolari
Ci sono delle grandezze dove le equivalenze richiedono calcoli diversi da quelli descritti fino a qui. Con le misure di tempo per esempio un minuto equivale a 60 secondi, perciò convertire un intervallo espresso in minuti richiederà di moltiplicare il valore per 60 e non per dieci. Lo stesso vale per ore e minuti, perché anche in questo caso convertire un valore nell’altro richiede di moltiplicare o dividere per 60.
Le equivalenze nella vita quotidiana
Un altro esempio è quando si deve scegliere che film vedere al cinema per scoprire che la durata è espressa in minuti (es. 135 minuti). Per capire con certezza a che ora si uscirà dalla sala torna utile saper convertire questo valore in ore (in questo caso, sono due ore e un quarto). O ancora quando si acquista una borraccia con la capacità espressa in centilitri (cl) per capire se travasando una bottiglia da mezzo litro l’acqua traboccherà o no.