Come calcolare la mediana in statistica

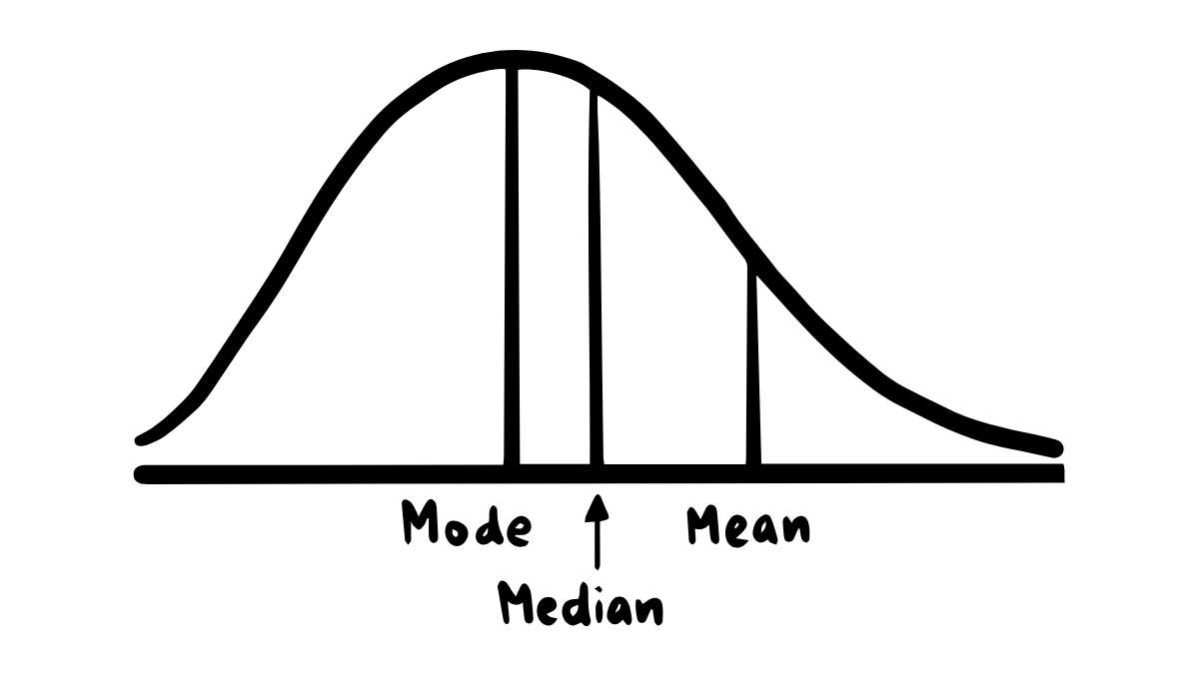
La definizione di questo concetto è il valore medio di un insieme di osservazioni ordinate in senso crescente. Con “medio” si intende la misura che si viene a trovare al centro di questa successione ordinata, che spesso e volentieri non coincide con la media. Si dice infatti che è un indice di posizione per una successione di valori, e la divide visivamente in due gruppi.

Passare dalla teoria alla pratica rende più semplice comprendere cosa sia la mediana, quindi prendiamo una serie Y di valori numerici interi.

Mettiamo Y = [3; 6; 8; 10; 13; 17; 24; 26; 29].
Come possiamo osservare si tratta di una serie già ordinata, perché i numeri si succedono in ordine crescente. Contandoli ricaviamo la numerosità n, che è pari a 9.

Dato che n è dispari possiamo usare la prima delle formule viste prima, perché avremo un solo valore al centro della successione.
Quindi facendo (9 + 1)/2 = 5, che corrisponde alla posizione che stiamo cercando. Partendo dal valore in posizione 1 (il 3) troviamo il numero 13 come quinto valore della successione. Se calcolassimo la media invece otterremmo una misura di gran lunga superiore, ossia 15,11.

Proviamo ora a calcolare la mediana di un insieme pari di valori, la successione X = [4; 7; 8; 12; 24; 19; 23; 30; 32; 35; 39; 43].
La numerosità qui è 12, dunque avremo due valori al centro della serie ordinata. In posizione centrale avremo quindi n/2 = 6, che è la posizione della prima misura, e n/2 + 1 = 7, quella dell’altra misura.
Quindi i valori 19 e 23, di cui possiamo fare la media ossia (19 + 23)/2 = 42/2 =21.

Fino a che abbiamo successioni di numerosità limitata non è difficile individuare anche solo a occhio la posizione della mediana. Se invece si ha a che fare con una distribuzione di classi di frequenza il discorso si complica. Prendiamo una distribuzione T del peso corporeo delle ragazze che frequentano una palestra suddivisa in cinque intervalli di peso (es. 40-50 kg, 50-60 kg ecc.)

 

Questo valore andrà confrontato con la stima delle frequenze cumulate  di ogni classe. Consideriamo per esempio il caso in cui il primo intervallo abbia Φi = 5, il secondo Φi = 10, il terzo Φi = 16. Il valore di Φμe risulterebbe pari a 15,5, ovvero compreso fra le frequenze delle classi numero 2 e 3. Il terzo intervallo sarebbe perciò la classe di Φμe.

La media si lascia facilmente influenzare da valori molto alti o molto bassi quando la numerosità campionaria è bassa, i cosiddetti outlier. Non sempre quindi descrive bene un insieme di dati, mentre l’indice di posizione che abbiamo esaminato finora non è così sensibile.

 

Come abbiamo visto conta solo la sua posizione nella successione ordinata, che è sempre quella centrale o le due centrali. I valori agli estremi non hanno alcun peso nel determinarla.

Possiamo fare un esempio, prendendo una serie con n = 5, ossia Z = [4; 5; 7; 9; 11]. Qui la mediana è il valore in terza posizione, ossia il 7. Ma anche sostituendo l’ultimo numero della successione con un valore molto più alto, come 145, non cambia nulla. Anche nella serie Z1 =[4; 5; 7; 9; 145] infatti il valore centrale rimane 7, come se non fosse variato nulla.

 

La proprietà di non cambiare anche in presenza di valori anomali rende la mediana una misura statistica di tendenza centrale più stabile della media, o meglio più “robusta”.
Questo permette di poterlo usare per avere più chiara la descrizione di un fenomeno quando la media tende a distorcerlo. L’esempio visto prima è un chiaro esempio di quando può verificarsi una situazioni di questo tipo.