La definizione in Fisica
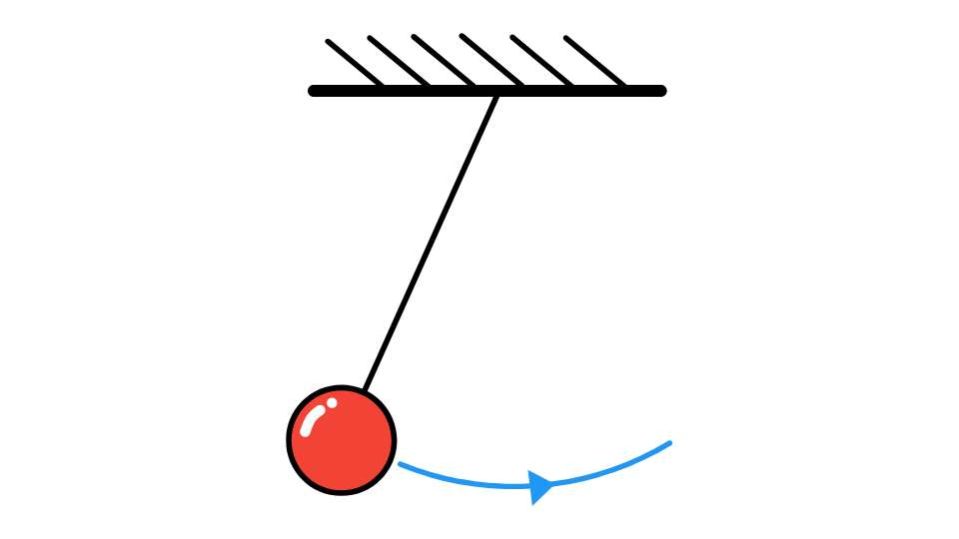
Se si parla di movimento si pensa subito a quello più semplice, che si compie lungo una linea retta. Tuttavia sappiamo che i corpi possono muoversi descrivendo diverse traiettorie, che possono essere curve o anche circolari. Se proiettiamo il movimento che si compie lungo un percorso a cerchio sul diametro dello stesso otterremo però quello che si definisce moto armonico. In altre parole è il diametro che rappresenta la sua traiettoria e ha un andamento oscillatorio.
Si tratta di un movimento che si può osservare facilmente in natura, per esempio quando consideriamo la propagazione del suono in aria o in acqua.
L’equazione oraria del moto armonico
Per prima occorre richiamare i concetti di periodo (T), frequenza (f) e la pulsazione (ω). Il primo rappresenta la durata di un’oscillazione completa rispetto al centro, la seconda il numero di oscillazione nell’unità di tempo (1 secondo) e l’ultima la velocità con cui si effettua un’oscillazione (si misura in radianti al secondo, rad/s). L’equazione oraria si esprime dunque nella forma x(t) = Acos(ωt +φ). Il simbolo A indica l’ampiezza delle oscillazioni di questo moto e si misura in metri, mentre φ è lo sfasamento eventuale che si misura sempre in radianti.
Partendo dall’equazione oraria possiamo ricavare anche la velocità e l’accelerazione del moto armonico, di cui vediamo di seguito le formule. Per la velocità abbiamo v(t) = Aωsen(ωt + φ) mentre per l’accelerazione a(t) = Aω2cos(ωt + φ). La velocità massima che un corpo può raggiungere nel corso delle oscillazione, ossia vmax, si trova invece moltiplicando l’ampiezza per la pulsazione.
La velocità del corpo che si muove oscillando risulta nulla a livello degli estremi dell’oscillazione, ovvero +A e -A. Nella direzione da +A a -A sarà negativa, mentre in direzione contraria avrà valori positivi. Per quanto riguarda l’accelerazione assume valore pari a zero nel centro di oscillazione e massima a livello degli estremi.
Dobbiamo anche precisare che la frequenza e il periodo in questa forma di movimento risultano del tutto indipendenti dall’ampiezza delle oscillazioni descritte. Per calcolare la pulsazione infatti tutto ciò che ci serve sapere sono la frequenza o il periodo, come vediamo dalle formule ω = 2πf e ω = 2π/T. Di conseguenza anche frequenza e periodo si possono ricavare a partire dalla velocità angolare, con le formule inverse T = 2π/ω e f = ω/2π.
La rappresentazione grafica
Ora che abbiamo definito i parametri che entrano in gioco nel moto armonico è ora di capire come lo si rappresenta sul piano cartesiano. Si ricorre a una funzione sinusoidale, fissando sull’asse delle ascisse il tempo e su quello delle ordinate la posizione assunta dal corpo che si sposta. Dopodiché si costruisce il sistema di riferimento considerando l’origine degli assi come il centro della circonferenza lungo cui si sposta il corpo. Il movimento quindi non partirà da O (0;0) ma da un punto sull’asse delle ordinate che dista dall’origine la misura del raggio della traiettoria circolare seguita.
Nel momento in cui il punto materiale con cui si fa coincidere il corpo compie un giro completo allora il grafico riparte dalla posizione iniziale. A metà del periodo il corpo si troverà in un punto situato al di sotto dell’asse delle ascisse distante da quest’ultimo una misura pari a -A. Quando il corpo si trova nel punto iniziale è all’inizio della circonferenza, e considerando l’angolo sotteso dall’arco descritto siamo su un angolo di 0°. Una volta che è terminata l’oscillazione e il corpo torna al punto di partenza ha percorso tutta la circonferenza, ossia un angolo di 360°.
Il moto armonico e le onde sonore
C’è infine il caso dove le onde sonore sono parzialmente fuori fase. Se lo sfasamento che esiste fra i due segnali non è completo ma è lieve allora ci sono frequenza che si sommano o si annullano in modo selettivo. Si ottiene così un suono disturbato, in cui ci sono momenti dove è difficile da sentire e altri in cui sembra il volume di alzi di colpo.
Le situazioni pratiche in cui possiamo avere interferenze distruttive o costruttive di solito sono i momenti in cui si effettuano delle registrazioni. Se i microfoni non sono posizionati correttamente o l’ambiente riflette i suoni è facile si creino differenze di fase.
L’oscillatore armonico
In questa formula k rappresenta la costante elastica della molla e x la variazione di lunghezza della molla determinata dalla forza. Se vogliamo determinare la pulsazione per l’oscillatore armonico vale la relazione ω = √k/m. Possiamo allora modificare l’equazione oraria vista in precedenza scrivendola nel formato x(t) = Acos(√k/mt +φ).