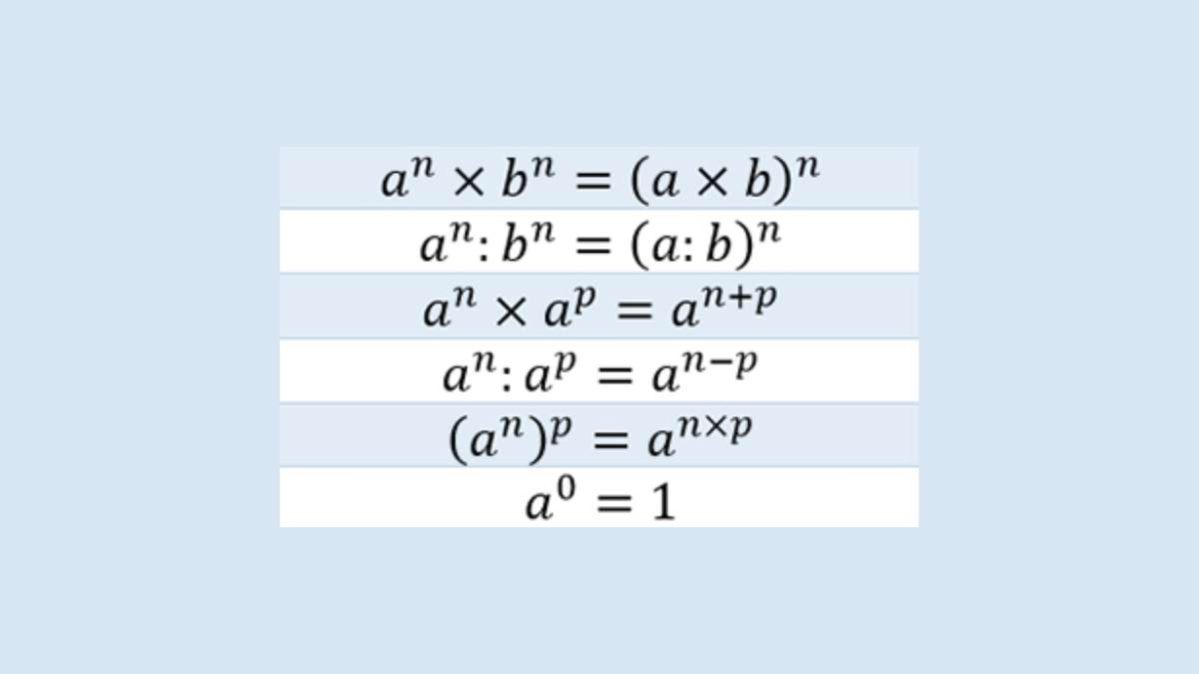Proprietà delle potenze: regole ed esempi

Cosa sono le proprietà delle potenze

Per capire cosa sono le proprietà delle potenze dobbiamo però innanzitutto partire dalle basi e trovare una definizione di “potenza”.

Con questo termine si intende una particolare operazione matematica, nella quale abbiamo una base, cioè un numero principale. Questo viene di solito moltiplicato per l’esponente.
Questo secondo numero di solito viene scritto in alto a destra della base e serve a indicare quante volte la base deve essere moltiplicata per se stessa.

La potenza è utile per la semplificazione dei calcoli: permette infatti di risolvere in maniera rapida equazioni e disequazioni.

I casi particolari

Ci addentreremo a breve nell’analisi delle proprietà delle potenze, ma prima dobbiamo analizzare alcuni casi particolari.

Se la potenza ha come base 1, il risultato sarà sempre 1.
Non importa quale sia l’esponente: in questo caso particolare, la soluzione è 1.

Abbiamo poi le potenze con esponente 0.
In questo caso, dato che ogni numero diviso per se stesso da 1, allora il risultato sarà sempre 1.

Infine, se sia la base che l’esponente sono uguali a 0, il risultato sarà indeterminato.

Le 5 proprietà delle potenze classiche

Quando parliamo di proprietà delle potenze, possiamo distinguere le cinque proprietà classiche, ossia quelle più comuni, dalle altre proprietà.

Quelle classiche sono le seguenti:

• prodotto di potenze con la stessa base
• quoziente di potenze con la stessa base
• prodotto di potenze con lo stesso esponente
• quoziente di potenze con lo stesso esponente
• potenza di potenza.

Di seguito, le analizzeremo tutte più nel dettaglio.

Prodotto di potenze con la stessa base

Quando ci troviamo a dover calcolare il prodotto tra due potenze con stessa base ma esponente diverso, tale prodotto sarà uguale a una potenza che ha come base la base stessa, con esponente la somma tra i vari esponenti.

In sostanza, tra le proprietà delle potenze questa è la proprietà che afferma che, se moltiplichiamo due (o più di due) potenze con base uguale ma esponenti diversi, ci basta lasciare la base immutata e sommare gli esponenti, per poi procedere al calcolo.

In formula, la regola del prodotto di potenze con la stessa base è la seguente:

• n^a ∙ n^b = n^a+b.

Per fare un esempio pratico, secondo questa proprietà avremo:

• 5² ∙ 5³ = (5 ∙ 5) ∙ (5 ∙ 5 ∙ 5) = 55

Quoziente di potenze con la stessa base

Allo stesso modo, quando ci troviamo a dover calcolare il quoziente tra potenze con stessa base ma esponenti diversi, tale quoziente sarà dato da una potenza che ha come base la stessa base, come esponente la differenza tra gli esponenti.

Detto in parole semplici, la proprietà delle potenze con base uguale ma esponente diverso ci dice che possiamo mantenere immutata la base, ma sottrarre i vari esponenti e poi procedere al calcolo.

In formula, questa regola viene scritta così:

• n^a : n^b = n^a-b

Se invece volessimo fare un esempio per comprendere meglio questa proprietà, potremmo dire che:

• 2⁷ : 2³ = 2⁴

Prodotto di potenze con lo stesso esponente

Anche quando ci troviamo a dover calcolare il prodotto di potenze con basi diverse ma esponente uguale possiamo ricorrere alle proprietà delle potenze.

In questo caso, il prodotto sarà dato da una potenza con esponente uguale, ma avente come base il prodotto delle basi.

La formula matematica per esprimere questa proprietà è la seguente:

• n^a ∙ m^a = (n ∙ m)^a = nm^a

Per fare un esempio, invece, possiamo dire che:

• 5² · 3² = (5 · 3)²

Quoziente di potenze con lo stesso esponente

Le proprietà delle potenze, poi, ci permettono di calcolare rapidamente il quoziente di potenze con base diversa, ma esponente uguale.

In questo caso, il quoziente sarà dato da una potenza con base che si ottiene dal quoziente delle basi e, come esponente, lo stesso esponente.

La proprietà viene espressa con la seguente formula matematica:

• n^a : m^a  = (n : m)^a = (n/m)^a

Per comprendere meglio questa proprietà, ecco poi un esempio concreto:

• 12³ : 3³ = (12 : 3)³

Potenza di potenza

La quinta e ultima tra le proprietà delle potenze è la cosiddetta potenza di potenza.

Quando ci misuriamo con una potenza di potenza, la base resta immutata; l’esponente della potenza, invece, è dato dal prodotto degli esponenti.

In sostanza, il risultato è dato da una potenza che ha base uguale alla potenza originaria. Per trovare l’esponente, invece, dovremo calcolare il prodotto tra gli esponenti.

La formula matematica di questa proprietà è la seguente:

• (n^a)^b = n^{a ∙ b}

Ecco poi un semplice esempio per comprendere meglio la regola:

• (2³)⁴ = 2¹²

Altre proprietà delle potenze

Quelle appena analizzate sono le proprietà delle potenze principali. Tuttavia, le potenze hanno anche altre proprietà.

Per esempio, nel caso di potenze con esponente negativo, bisognerà calcolare la potenza del reciproco di quel numero.

In formula matematica, questa proprietà si traduce così:

• a⁻ⁿ = 1 / aⁿ (con a ≠ 0)

Ed ecco un esempio per meglio comprendere la proprietà:

• 2⁻³ = 1 / 2³ = 1/8

Infine, quando una potenza ha un esponente frazionario, il risultato è un radicale. L’indice della radice è il denominatore della frazione, mentre l’esponente del radicando è il numeratore della frazione.

La formula matematica generale è la seguente:

• a^(m/n) = √n (con a ≥ 0)

Anche in questo caso, lasceremo un esempio numerico al quale abbiamo applicato la formula matematica generale:

• 9^(1/2) = √9 = 3