Qualche cenno sullo scienziato
Dire teorema di Torricelli senza aggiungere altri dettagli può confondere dato che questo studioso fu sia un fisico che un matematico. Di seguito analizzeremo la formula che permette di calcolare il flusso di uscita di un liquido da un contenitore, ma a Evangelista Torricelli riconduciamo anche il teorema fondamentale del calcolo integrale. Per calcolare gli integrali definiti è fondamentale perché stabilisce una relazione tra questi e le derivate di una funzione.
Tornando alla Fisica, questo scienziato italiano è ricordato anche per aver definito una delle unità di misura usate per la pressione, ovvero il millimetro di mercurio (mmHg). Un’atmosfera (1 atm) corrisponde a 760 mmHg, o torr (da Torricelli), come si evince dalla sua invenzione del barometro a mercuri
Cosa afferma il teorema di Torricelli
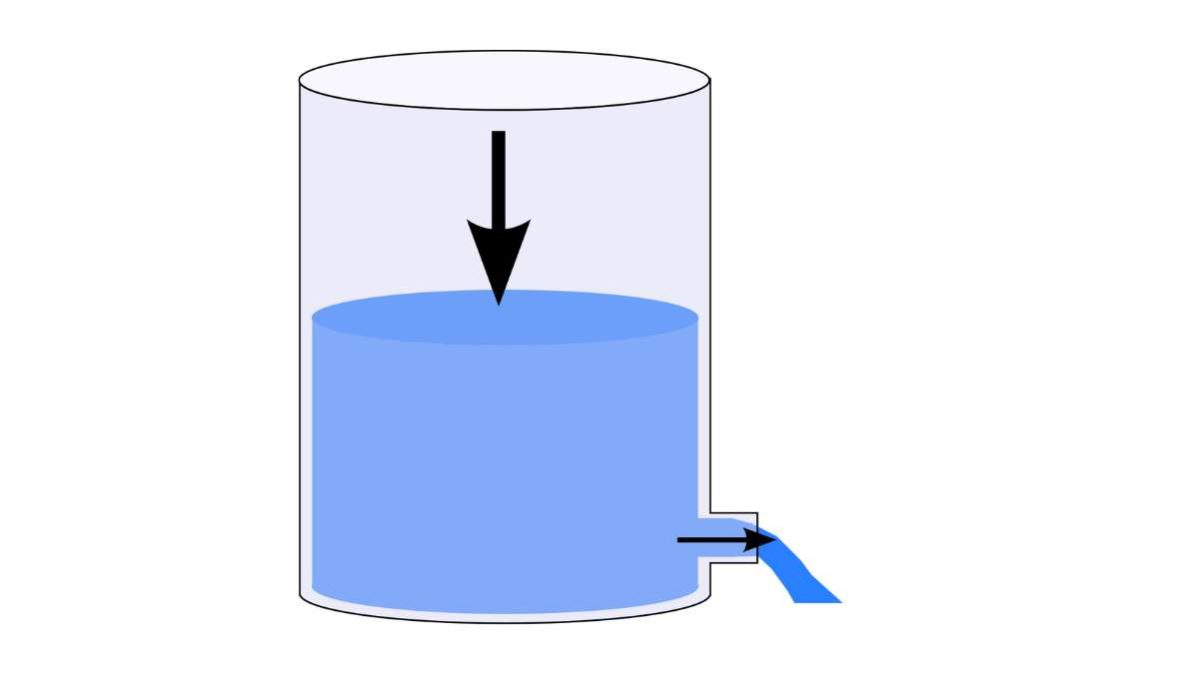
In fluidodinamica ricorriamo a questa legge per determinare la velocità del flusso di un liquido sotto determinate circostanze. Vale a dire quando abbiamo un contenitore pieno dove si apre un foro e il suo contenuto inizia a defluire all’esterno.
La pressione che il liquido esercita sulle pareti del contenitore lo porta a uscire formando un getto che può avere velocità variabile. Prendendo l’esempio di una colonna d’acqua dovremmo aspettarci una variazione in base all’altezza a cui si pratica il foro. La pressione idrostatica infatti aumenta in parallelo alla profondità, o meglio all’altezza della colonna d’acqua che preme sul punto considerato.
La formula per il calcolo della velocità stabilita dal teorema di Torricelli è v = √2gh.
Mentre g è la costante di gravità il fattore h rappresenta per l’appunto la profondità a cui il punto dove pratichiamo il foro si trova rispetto alla superficie del liquido. Per valere è necessario però considerare un’ipotesi di partenza ben definita relativa alla grandezza del foro che pratichiamo sul contenitore.
Vale a dire che deve essere molto piccola rispetto alla superficie libera del liquido, che si abbasserà via via che il flusso procede. In questo modo la velocità con cui il liquido uscirà sarà molto più alta di quella con cui la superficie libera si abbasserà.
La dimostrazione con l’equazione di Bernoulli
In entrambi i punti considerati, ovvero la superficie libera del liquido e il foro la pressione coinciderà con quella atmosferica, così come la densità. Considereremo nulla la velocità con cui il liquido si abbassa e quindi nell’equazione avremo solo la velocità del flusso di uscita.
Quindi otteniamo in superficie P + ρgh e a livello del foro P + 1/2ρv2. Otteniamo perciò P + ρgh = P + 1/2ρv2. Possiamo semplificare ulteriormente rimuovendo P e dividendo entrambi i membri dell’equazione per ρ, e rimane gh = 1/2v2.
Ora per trovare v non dobbiamo fare altro che spostare gh a destra dell’uguale, moltiplicare per due ed estrarre la radice del risultato. Così torniamo alla formula vista prima, ossia v = √2gh.
Un esercizio sul teorema di Torricelli
Le applicazioni di questa legge dell’idrodinamica
Conoscere il teorema di Torricelli è alla base della progettazione di strutture imponenti quali sono ad esempio le dighe che delimitano i bacini che servono per le centrali idroelettrica.
Quando si crea un lago artificiale bisogna infatti considerare la pressione dell’acqua che andrà a premere contro la barriera per essere sicuri che resista nel tempo. Per prevenire il sovraccarico sulla diga si prevede infatti una struttura detta spillway.
Si tratta nel dettaglio di un canale attraverso cui si fa defluire l’acqua in eccesso nel momento in cui la pressione che il liquido esercita rischia di creare crepe o cedimenti nella struttura.
Possiamo avere spillway di controllati meccanicamente tramite valvole o cancelli, che si possono aprire a richiesta. Spesso però se ne prevedono anche di liberi, dove semplicemente l’acqua fluisce spontaneamente superato un certo livello senza richiedere monitoraggio da parte del personale della centrale.
Controllare la portata e la velocità dell’acqua che defluisce è essenziale per una produzione efficiente di energia idroelettrica. Questo naturalmente vale per le centrali a bacino, ma ci sono anche impianti idroelettrici che sfruttano l’acqua fluente, come quella di un fiume o un torrente.