Le scoperte astronomiche del 1600
Secondo quanto risulta agli storici le leggi di Keplero furono definite fra il 1608 e il 1619, periodo in cui l’astronomia fu una materia scientifica di grande interesse. Come dice il nome a scoprirel fu Johannes Keplero, scienziato, filosofo e teologo tedesco che riprese la teoria dell’eliocentrismo definita da Copernico. I suoi studi astronomici si focalizzarono infatti sulla natura del moto dei pianeti intorno al sole.
Anni prima della definizione dei principi che studiamo ancora oggi lo studioso aveva pubblicato un trattato scientifico dal titolo Mysterium Cosmographicum. Alcuni dei concetti qui elaborati però li rivide del tutto, come l’idea delle orbite disegnate come forme solide regolari.
La prima delle leggi di Keplero
L’enunciato di questo principio afferma che le orbite descritte dai pianeti intorno al sole hanno forma ellittica, dove la stella occupa la posizione di uno dei due fuochi. Per questo motivo la si definisce anche legge delle orbite ellittiche. Di conseguenza il Sole non si trova al centro di ogni orbita ma in un punto che rispetta un’altra condizione rispetto al percorso del pianeta. I fuochi sono infatti i punti situati sull’asse maggiore per cui la somma delle distanze da qualsiasi punto dell’ellisse è constante.
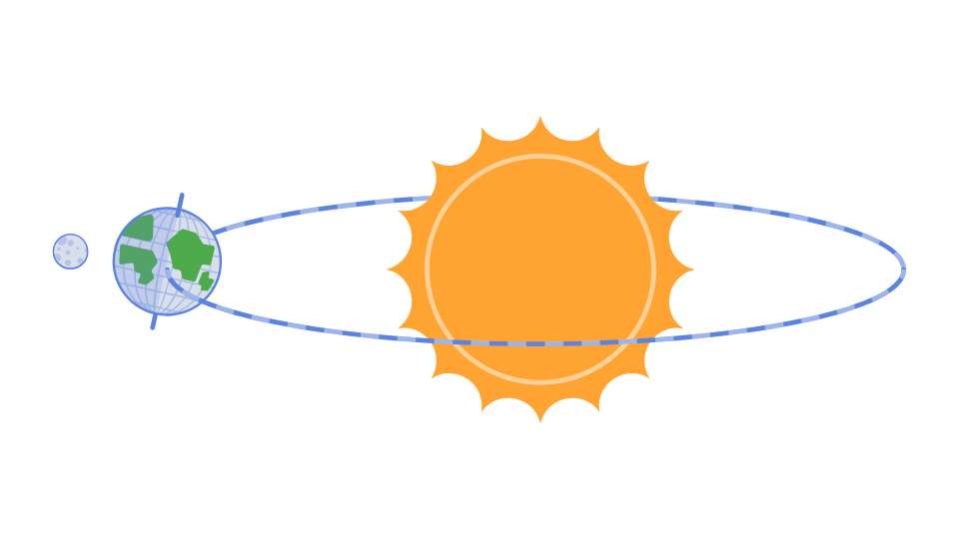
All’interno della prima delle leggi di Keplero si definiscono anche i concetti di perielio e afelio. Il perielio corrisponde al punto dove la distanza del corpo celeste che segue l’orbita dal sole ha il suo valore più basso. Quando invece il pianeta raggiunge il punto più lontano dalla stella senza uscite dall’orbita invece significa che si trova nell’afelio. Nel caso della Terra al perielio la distanza fra il pianeta e il Sole è di 147 milioni di km, che sale a 152 quando giunge nel suo afelio.
La principale conseguenza che si deduce di questo principio c’è perciò il fatto che la distanza di un pianeta dal Sole vari di continuo. Anche se nasce per spiegare il moto dei pianeti è possibile applicarla anche ad altri corpi celesti tra cui per esempio i satelliti. Dobbiamo considerare che per ogni corpo celeste considerato ci siano valori diversi di eccentricità dell’ellisse. Si tratta della grandezza che esprime il grado di “schiacciamento” della curva. Di conseguenza alcune orbite saranno quasi circolari, come nel caso del nostro pianeta.
Il principio delle aree
Arriviamo alla seconda delle leggi di Keplero, il cui enunciato afferma che il raggio vettore che congiunge un pianeta e il sole descrive aree uguali in tempi uguali. Si definisce raggio vettore il segmento che congiunge un pianeta al Sole e che mentre questo si muove si sposta a sua volta individuando dei settori. Dato che la stella si trova in uno dei due fuochi dell’ellisse è chiaro che il raggio vettore sarà più corto nei pressi del perielio. Viceversa si allungherà man mano che il corpo celeste procederà verso l’afelio.
Per descrivere aree uguali negli stessi tempi perciò la velocità dei pianeti non sarà la stessa in tutti i punti dell’orbita. La lunghezza del raggio vettore e la velocità del corpo celeste risultano perciò inversamente proporzionali fra di loro. Vicino al perielio il pianeta si muoverà più lentamente, in virtù anche della maggiore attrazione gravitazionale. Man mano che seguendo l’orbita si allontanerà dal Sole invece si muoverà sempre più veloce fino a toccare il valore massimo nell’afelio.
Possiamo scrivere in formula la seconda delle leggi di Keplero usando dA/dt = k. Considerando A come l’area descritta dal raggio vettore e t come il tempo considerato avremo che il loro rapporto risulta costante. Quando approssimiamo l’orbita a una circonferenza possiamo far coincidere il raggio vettore con il semiasse maggiore dell’ellisse. Le uniche eccezioni sono i percorsi orbitali di Mercurio e di Plutone, che appaiono più appiattiti verso l’asse maggiore rispetto a quelli degli altri pianeti.
La legge dei periodi
Per definire questa ultima legge lo scienziato raccolse i dati a disposizione relativi sia alla distanza dei pianeti dal Sole che i periodi di rivoluzione e li riportò su di un grafico. Da qui rilevò che non si potevano osservare né relazioni lineari né di crescita esponenziale. Da un’analisi più approfondita ricavò che è possibile definire un rapporto di proporzionalità tra il quadrato del periodo di rivoluzione di un pianeta e il cubo della sua distanza dalla stella. In formula indichiamo con T il periodo di rivoluzione e con r la distanza, ottenendo T2= r3k.
La terza delle leggi di Keplero ci mostra quindi che il rapporto fra T2 e r3 è costante per tutti i pianeti. Il valore della costante k invece si può ricavare comparando fra loro la forza gravitazionale e la forza centripeta a cui sono soggetti i pianeti. Ne ricaviamo che il valore della costante è pari a 4π2/GMsole. In questa formula G rappresenta la costante di gravitazione universale e il suo valore è 6,67 x 10-11 N·m2/kg2.
Limiti delle leggi di Keplero
Un altro problema è che nel caso del Sistema Solare abbiamo ben 7 pianeti che orbitano intorno alla stessa stella. Le interazioni con altri corpi celesti però non sono considerate nelle leggi appena viste quindi anche queste devono risultare trascurabili. La presenza di altri pianeti o satelliti infatti porta a leggere variazioni nella forma dell’orbita descritta oltre che nella velocità di rotazione.