Le definizioni in Geometria
Per prima cosa possiamo distinguere fra loro questi due concetti individuando nella prima la linea di confine e nella seconda la figura geometrica nel suo insieme. Il cerchio infatti rappresenta la parte di piano compresa all’interno della circonferenza, mentre quest’ultima rappresenta il luogo dei punti equidistanti dal centro del cerchio. Unendo il centro a uno qualsiasi dei punti di questa linea infatti si avrà un segmento sempre della stessa lunghezza, che corrisponde al raggio del cerchio.
Vedremo di seguito le formule geometriche per calcolare entrambi oltre a qualche esempio pratico per capire come andare ad applicarle negli esercizi.
La circonferenza, un perimetro senza lati
Dato che al suo interno delimita una superficie piana coincide con il perimetro del cerchio. Possiamo anche immaginarla come un poligono regolare con i lati così corti che si riducono alla dimensione di un punto, fino a formare un’unica linea chiusa di forma circolare. Non essendoci lati visibili però non possiamo sommarne le lunghezze e serve cercare una formula diversa.
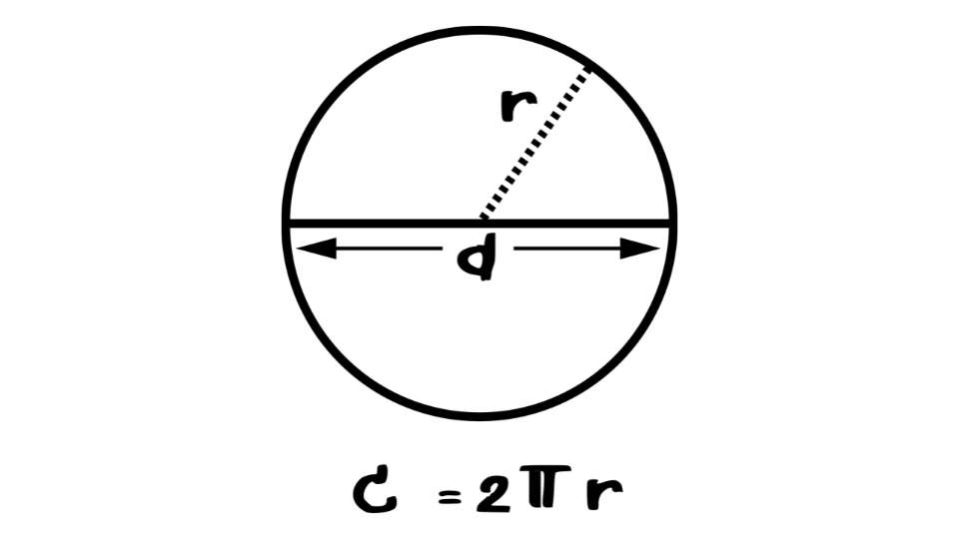
Abbiamo già accennato al raggio, il segmento che unisce centro del cerchio e un punto qualsiasi del bordo. Dobbiamo introdurre ora il concetto di diametro, che dal punto di vista pratico è semplicemente il doppio del raggio. Per definizione però si tratta della corda massima di un cerchio, passante per il suo centro. Il rapporto tra una circonferenza (C) e il suo diametro (d) è sempre equivalente a π, valore che arrotondiamo a 3,14. In formula quindi possiamo die che C = πd.
Supponendo di avere un cerchio dove sappiamo che il diametro è di 8 cm per ricavare la misura del suo perimetro dovremo fare 8 x 3,14 = 25,12 cm. Se invece è noto il raggio (r) bisogna raddoppiarlo e poi moltiplicare il risultato sempre per il valore di π. Possiamo perciò ricavare anche una seconda formula, ovvero C = 2rπ. Per disegnare una circonferenza in effetti si parte di solito da un punto come centro e si definisce la misura del raggio per poi tracciarla con il compasso.
La superficie del cerchio
Dopo aver capito come ricavare la misura della circonferenza è ora di dedicarsi all’area che questa linea curva va a individuare. Anche in questo caso ritorna il valore di π, in quanto per trovare la superficie (S) del cerchio è S = r2π. Tutto ciò che ci serve sapere quindi è la misura del raggio essendo π una costante. Secondo il metodo individuato dal matematico greco Archimede potremmo anche dire che il cerchio è equivalente a un triangolo dove l’altezza è il raggio mentre la base risulta pari alla misura di C.
Vediamo però il caso dove compaiono due cerchi concentrici, ovvero dove ci sono il centro in comune ma diverse misure di raggio. Graficamente si ottiene un anello tra il cerchio interno e la circonferenza di quello esterno, che si definisce corona circolare. Anche per il calcolo di questa superficie (SC) esiste una formula, ovvero SC = π(R2 – r2). Con R indichiamo il raggio del cerchio più ampio e con r quello del cerchio minore.
Supponiamo di avere una circonferenza di raggio 9 cm e una di raggio pari a 4 cm concentriche fra di loro. Per trovare l’area della corona circolare che descrivono dovremo usare la formula vista sopra e quindi SC = π(92 – 42) = 3,14 x (81 – 16) = 204,1 cm². Di base potremmo anche ricavare la superficie del cerchio più piccolo e sottarla all’area del cerchio esterno, e la formula non è che una semplificazione di questo calcolo.
La circonferenza come equazione cartesiana
Abbiamo visto come calcolare la lunghezza della linea che delimita il cerchio, ma ora vediamo come si presenta questa curva in forma canonica. Se vogliamo tracciarne una nel piano cartesiano ci servono almeno tre punti, e l’equazione per determinarli si presenta nella forma x2 + y2 + ax + by + c = 0. Scritta così appare nella forma più generale possibile, ma se abbiamo già un centro determinato la possiamo trovare scritta in un altro modo.
Una circonferenza di centro (C) e raggio (r) noto avrà come equazione la forma (x – xC)2+ (y – yC)2= r2. Sviluppandola possiamo arrivare alla forma x2 + y2 -2xCx – 2yCy + (xC2 + yC2 – r2) = 0. Da questa formula possiamo determinare come trovare i coefficienti a, b e c. Ovvero a = -2xC, il termine b = -2yC e infine c =xC2 + yC2 – r2. Per ricavare le coordinate del centro del cerchio avremo le formule xC = -a/2 e yC = -b/2, mentre il raggio si ricava facendo r = √a2/4 + b2/4 – c.
Vediamo un esempio pratico, dove sappiamo che il centro di un cerchio si trova nel punto P(2;3) e la lunghezza del suo raggio è pari a 5 cm. L’equazione del suo perimetro sarà x2 – 4x -6y + y2+ 13 – 25 = 0, che semplificata sarà x2 + y2 -4x – 6y -12 = 0. Se invece ci viene fornita l’equazione canonica della curva, per esempio x2 + y2 -8x – 2y – 8 = 0. Per trovare il centro faremo C = (+8/2; +2/2) =(4; 1), mentre la lunghezza del raggio sarà r = √64/4 + 4/4 + 8 = √16 + 1 + 8 = √25 = 5 cm.
La rappresentazione come sezione conica
Indicando con α l’angolo che l’apotema del cono forma con l’asse centrale e con β quello assunto dal piano che lo interseca possiamo determinare quale delle altre curve si otterrà confrontandoli. Per esempio se le due ampiezze coincidono si ottiene una parabola.