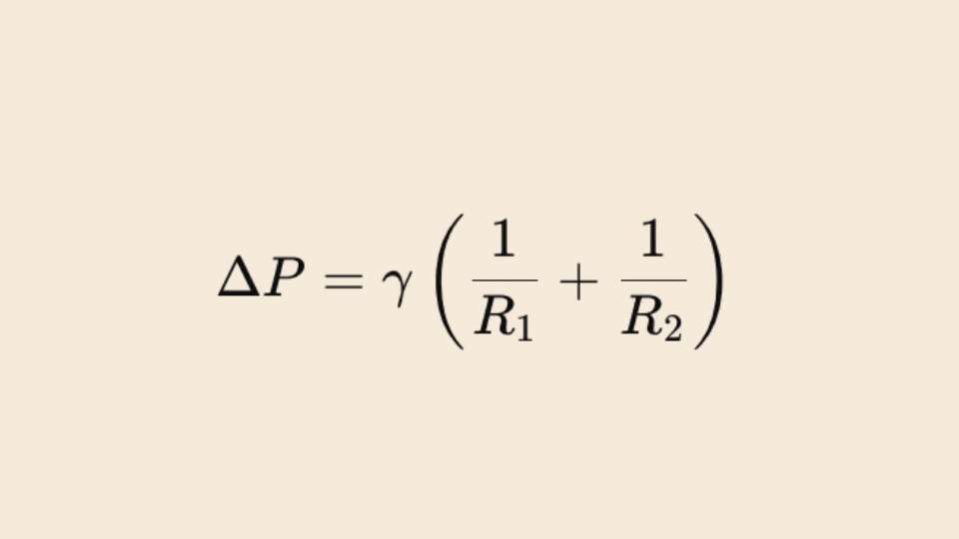La legge di Laplace in Fisica
Questo principio prende il nome dal marchese Pierre-Simon Laplace, matematico e fisico francese che operò nel periodo napoleonico, ma più spesso è indicato come equazione di Laplace. La sua funzione è quella di inquadrare la relazione che in un fluido intercorre fra la tensione superficiale, la pressione e il raggio di curvatura.
Si utilizza per definire due fenomeni in particolare, ovvero il passaggio all’interno di condotti di fluidi sotto pressione e la formazione di bolle. Per questo si sfrutta sia nella progettazione di impianti che nel trattamento di alcune condizioni cliniche.
Le diverse forme dell’equazione
Vediamo come si esprime la legge di Laplace in base al caso che si sta considerando. Se stiamo studiando il comportamento di un fluido all’interno di un tubo a sezione cilindrica l’equazione appare nella forma ΔP=2t/r. In questa formula ΔP rappresenta la differenza di pressione fra le due interfacce di una superficie curva e t la tensione superficiale del fluido, mentre r è il raggio della curvatura.
Se invece consideriamo una sfera o una superficie che ha una curvatura bidimensionale l’equazione si presenta come ΔP=4t/r. Degli esempi pratici di questo caso sono le bolle che si formano in un fluido oppure un palloncino pieno d’acqua o di un altro liquido.
La tensione superficiale è la forza di coesione fra le particelle della superficie di un fluido, che sull’acqua possiamo osservare quando vediamo che sopra di essa si muovono i ragni d’acqua (detti anche gerridi). Dato che la si indica spesso anche con il simbolo σ la legge di Laplace per i due casi precedenti si può riscrivere in un modo diverso. Per i cilindri ΔP = 2σ/r e per le sfere invece ΔP = 4σ/r.
Applicazioni della legge di Laplace in Biologia
Abbiamo detto che questo principio torna utile per capire la dinamica dei fluidi che scorrono all’interno di condotte. Anche i nostri vasi sanguigni possono essere equiparati a delle tubature, anche se hanno la particolarità di non essere rigidi. Quando applichiamo l’equazione alle vene o alle arterie è per determinare la loro tensione parietale (T). A generarla è sia la contrazione della muscolatura liscia presente nella parete che l’elasticità del vaso sanguigno.
La formula per ricavarla è T = Ptmr/d. Come nell’equazione vista prima r rappresenta il raggio del vaso sanguigno considerato, mentre d è lo spessore della parete, che varia fra arterie, vene e capillari. Infine Ptm rappresenta la forza distendente a cui è sottoposta la parete del vaso. Se la tensione parietale non riesce a sostenere la forza distendente si rischia la rottura della parete dell’arteria o della vena.
In questo senso la legge di Laplace permette di comprendere perché si verifica la rottura di un aneurisma. Dal punto di vista medico si tratta di una dilatazione anomala ma permanente della parete di un’arteria o di una vena. Si forma in seguito a un trauma o a patologie che provocano un’indebolimento del vaso sanguigno, e se si rompe può provocare emorragie gravi se non letali.
Un aneurisma vede un aumento del raggio e una diminuzione dello spessore della parete, che diventa più fragile. Per contrastare la Ptm occorre un aumento della T, e se questa risulta insufficiente si verifica la rottura della parete e la fuoriuscita del flusso ematico. La formula vista applicata ai vasi spiega anche come mai i capillari resistano anche a pressioni elevate .Avendo un raggio piccolo basta una T bassa.
L’applicazione dell’equazione agli alveoli polmonari
Possiamo rifarci all’equazione ΔP = 2σ/r, che afferma che la pressione sia inversamente proporzionale al raggio dell’alveolo considerato. Quando abbiamo degli alveoli piccoli collegati ad alveoli più grandi l’aria dovrebbe fluire dai primi agli altri, provocandone il collasso.
La presenza del surfattante però crea una tensione superficiale che inverte questa tendenza, come ricaviamo dalla legge di Laplace. Ogni alveolo infatti contiene la stessa quantità di questo fluido, a prescindere dal raggio. Dunque il surfattante risulterà più concentrato negli alveoli più piccoli perché ha una minore superficie a disposizione su cui posizionarsi. Il flusso d’aria quindi finisce con il cercare di bilanciarsi fra due alveoli e questi arrivano ad avere più o meno tutti lo stesso raggio.
Il surfattante si inizia a produrre all’interno dei polmoni del feto durante il settimo mese di gestazione. Il primo respiro del neonato riempie d’aria gli alveoli per la prima volta, creando la pressione interna.
La legge di Laplace e l’estrazione del petrolio
In più dalla formula della legge di Laplace applicata alle sfere (ΔP=4t/r) ricaviamo un secondo dettaglio. Ovvero che a un recipiente di questo tipo serve solo metà della tensione di parete richiesta da un recipiente cilindrico con medesimo raggio e soggetto alla stessa pressione. Per risparmiare sull’impiego dei materiali e sui costi quindi i recipienti soggetti ad alte pressioni si progettano di forma sferica. L’efficienza è maggiore e questa scelta consente di contenere i costi. Naturalmente dipende anche dai materiali utilizzati.
Sono in particolare le condutture utilizzate nei pozzi petroliferi che per funzionare devono rispettare la relazione descritta dall’equazione.