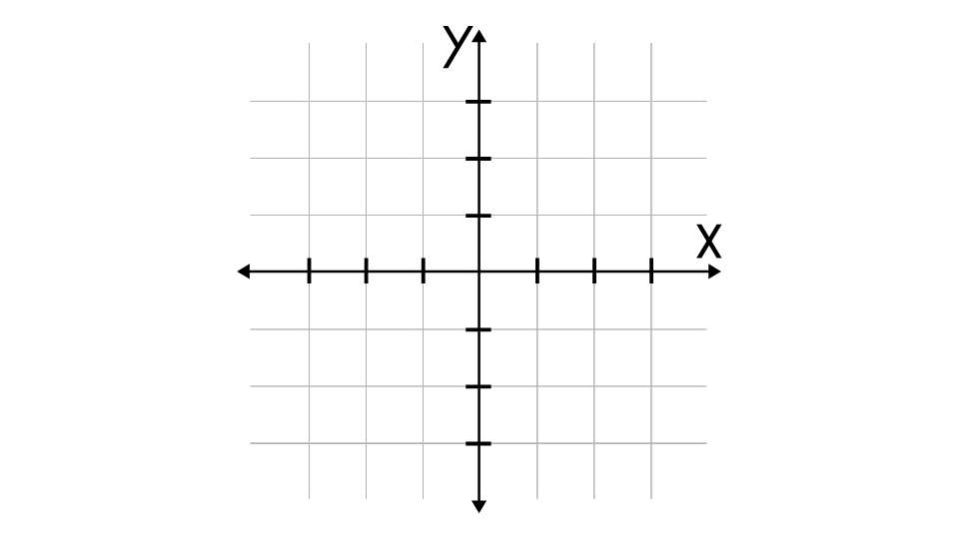
Cos'è il piano cartesiano
Questo argomento spesso si introduce già alle elementari e si tratta di un sistema di rappresentazione Oxy. Ovvero è presente un punto di origine e in genere due coordinate per individuare la posizione degli oggetti o dei punti che si disegnano al suo interno. Si usa in geometria analitica per rappresentare figure piane, ma aggiungendo una terza coordinata (z) torna utile anche per i solidi geometrici.
Di seguito vedremo come utilizzare questo sistema per rappresentare punti e rette, che poi è la base necessaria per costruire i grafici.
Il punto di origine e gli assi x e y
Abbiamo detto che il piano cartesiano studiato nella sua forma base prevede due coordinate. Le x, dette anche ascisse, i cui valori si rappresentano su un asse orizzontale che parte dall’origine prosegue in entrambe le direzioni (destra e sinistra) potenzialmente all’infinito. Poi troviamo le y, o ordinate, che invece sono i valori della retta verticale e determinano la posizione verso l’alto o verso il basso rispetto all’origine.
L’asse delle ascisse e l’asse delle ordinate sono perpendicolari fra di loro e si incontrano nel punto di origine. Ogni punto all’interno del piano si identifica attraverso un valore di ascissa (x) e uno di ordinata (detto y). L’origine (punto O) corrisponde al valore 0 per entrambe le coordinate, quindi avremo O (0;0). Per scrivere le coordinate del piano cartesiano infatti si indica prima l’ascissa e poi l’ordinata, separate da un punto e virgola e tra due parentesi tonde.
Dal punto O gli assi x e y proseguono all’infinito, quindi possiamo avere anche coordinate negative. Quando rappresento qualcosa a sinistra dell’origine la sua x sarà negativa, così come quando sarà posizionato più in basso del punto O avremo y con valore negativo. Prolungando i due assi costruiamo una croce che individua quattro aree, o quadranti. Li numeriamo da I a IV considerando quello in alto a sinistra come primo.
Rappresentare i punti nel piano cartesiano
Suddividendo l’unità di misura è possibile riportare anche valori razionali (1,5, 3/4 ecc.). La maniera più semplice è rappresentare il piano cartesiano sulla carta quadrettata, in modo che ogni quadretto corrisponda a 1 e sia più facile individuare la posizione corretta.
Quando l’ascissa è pari a zero, come per il punto A (0; 4) il punto andrà posizionato sull’asse delle ordinate dopo quattro unità di misura. In caso invece sia l’ordinata pari a zero, come per il punto B (5;0), il punto andrà segnato sull’asse delle ascisse.
Come si rappresenta una retta
Anche se come sappiamo una retta è una successione illimitata di punti, per disegnarla ne sono sufficienti due. Una volta ricavati è sufficiente disegnarli nel piano cartesiano e tracciare una linea che passi per entrambi, proseguendo virtualmente all’infinito in entrambe le direzioni. Se i due punti non sono già noti ma si conosce l’equazione della retta allora si possono ricavare con un semplice calcolo.
L’equazione di una retta generica è y = mx + q, dove m rappresenta il coefficiente angolare e q l’ordinata all’origine. Questo significa che quando a x si assegna il valore zero allora il valore di y coinciderà con q. Prendiamo ora un esempio, ossia la retta y = 2x + 1. Se ci venisse chiesto di rappresentarla dovremmo trovare almeno due punti per cui passerà.
Per farlo non serve altro che sostituire alla x due valori a libera scelta. In questo caso potremmo scegliere 1 e 2.
A questo punto sostituiamo nell’equazione y = 2 x 1 + 1 = 2 + 1 = 3 e successivamente y = 2 x 2 + 1 = 4 + 1 = 5. Nel piano cartesiano perciò dovremo disegnare i due punti A (1 ; 3) e B (2 ; 5). Non serve per forza utilizzare numeri interi positivi, si possono utilizzare anche numeri relativi o razionali.
I segmenti nel piano cartesiano
Se per disegnare una retta bastano due punti, disegnarne due con coordinate casuali e unirli fra loro fa ottenere un segmento. I punti allora si dicono estremi del segmento, una linea finita che simboleggia la loro distanza. Se i punti hanno la stessa ordinata o la stessa ascissa è facile determinarne la lunghezza, ma se non è così esiste una formula apposita.
Per trovare la lunghezza del segmento che unisce un punto A(xA ; yA) e B (xB ; yB) possiamo calcolare la loro distanza d = √(xB – xA)2 + (yB – yA)2.
Prendiamo ad esempio due punti A (4; 2) e B (6; 4) e sostituiamo le loro coordinate nell’equazione. Avremo allora d = √(6 – 4)2 + (4 – 2)2 = √4 + 4 = √8.
Nel caso in cui come accennato abbiamo due punti nel piano cartesiano con ordinata o ascissa uguali il calcolo della lunghezza del segmento si semplifica. Consideriamo A (2; 5) e B (2; 7) e usiamo sempre la stessa formula d = √(2 – 2)2 + (7– 5)2 = √0 + 4 = √4 = 2. Come si può notare uno dei due termini sotto radice infatti inevitabilmente risulta uguale a zero.
Ricavare il punto medio di un segmento
Come si può trovare la distanza fra due punti con una semplice formula così nel piano cartesiano esiste un sistema per determinarne il punto medio. Si tratta del segno che divide in due metà perfettamente uguali il segmento che unisce due punti. Tutto ciò che serve è conoscere le coordinate degli estremi della linea.
Servono per la precisione due formule per trovare il punto medio M del segmento che unisce due punti generici A e B. La sua ascissa xM si poteva trovare con il calcolo (xA + xB)/2, e per la sua ordinata yM invece la formula (yA + yB)/2.