Seno e coseno: proprietà e usi delle due funzioni fondamentali della trigonometria
Nella matematica, seno e coseno sono due funzioni fondamentali della trigonometria, nate dall’esigenza di studiare i rapporti tra i lati di un triangolo rettangolo in relazione ai suoi angoli.
Questi concetti, apparentemente teorici, in realtà hanno un’applicazione molto pratica: ci permettono di misurare e comprendere fenomeni che vanno ben oltre la geometria pura. Dal calcolo delle altezze e delle distanze, fino alla descrizione di onde, oscillazioni e movimenti periodici, le funzioni seno e coseno sono strumenti essenziali in fisica, ingegneria, informatica e persino in grafica digitale.
In questo articolo andremo a scoprire in modo chiaro e semplice che cosa rappresentano il seno e il coseno, come vengono definiti all’interno del cerchio goniometrico e perché risultano così importanti nello studio delle funzioni matematiche. Un viaggio che ci aiuterà a collegare la teoria alla realtà, comprendendo meglio non solo il funzionamento di queste formule, ma anche le loro applicazioni quotidiane.
Che cosa sono le funzioni seno e coseno
Seno e coseno sono due funzioni trigonometriche fondamentali che permettono di comprendere fenomeni periodici, oscillazioni, e molteplici situazioni geometriche e fisiche.
Per poterli definire occorre pensare a un angolo posto in un sistema di coordinate cartesiane: si traccia un raggio partendo dall’origine e formando un angolo con l’asse delle ascisse, e si osservano le coordinate del punto che questo raggio incontra sulla circonferenza goniometrica, ovvero la circonferenza di raggio unitario centrata nell’origine. Il valore del coseno corrisponde proprio all’ascissa di quel punto, mentre il valore del seno corrisponde all’ordinata.
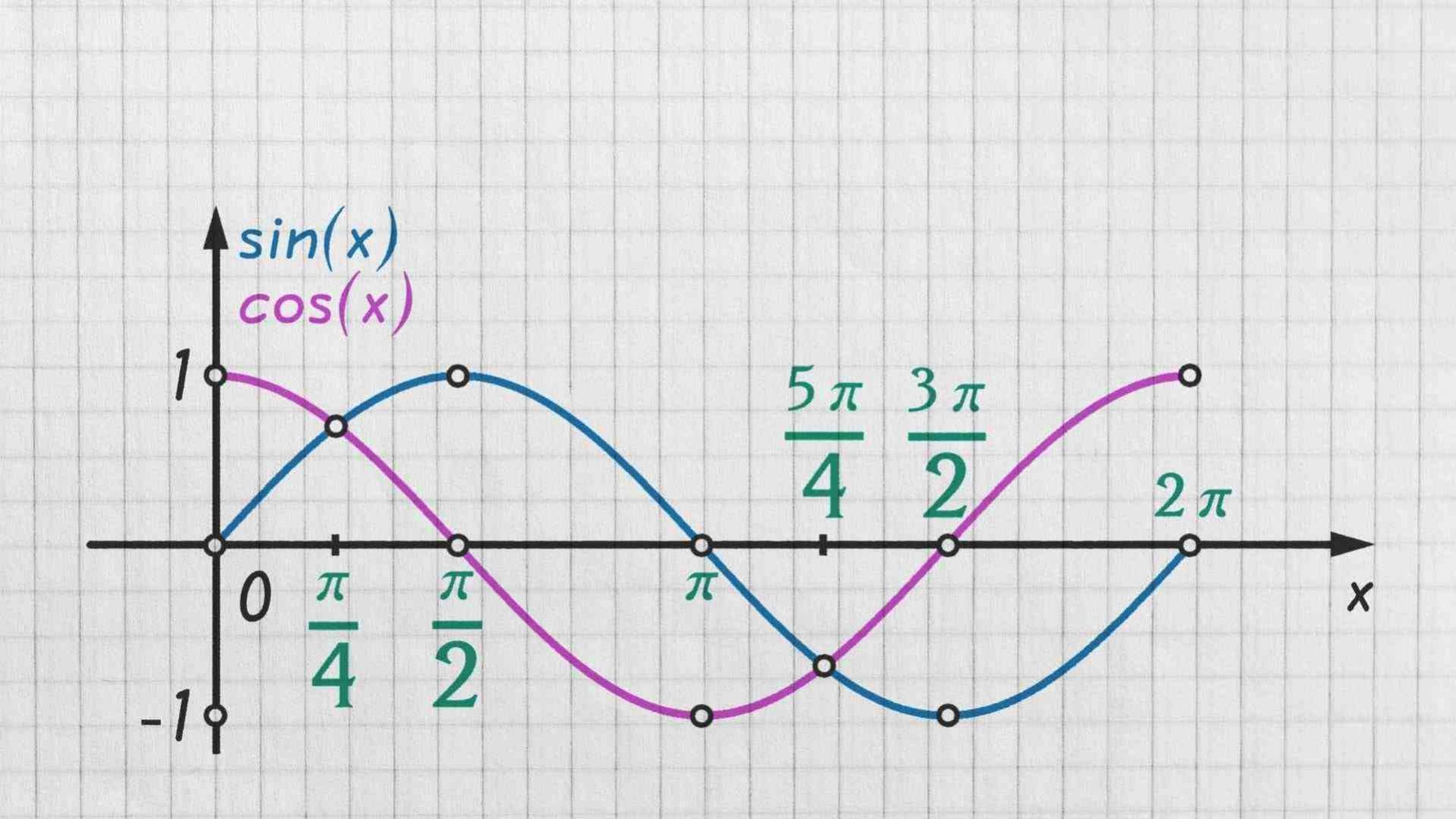
Procediamo con un esempio pratico per comprendere al meglio il difficile concetto. Dato un angolo di 0°, il punto sulla circonferenza goniometrica si trova sull’asse orizzontale destro, quindi il coseno vale 1 e il seno 0. Se invece l’angolo è di 90°, il punto si sposta sull’asse verticale, così il seno vale 1 e il coseno 0.
In questo modo, seno e coseno non sono più legati esclusivamente a triangoli rettangoli, ma possono essere estesi a qualsiasi angolo, anche maggiore di 90°, e assumere valori positivi o negativi a seconda del quadrante in cui si trova il punto sulla circonferenza.
A livello generale, questa interpretazione geometrica è la base per molte proprietà e applicazioni successive, in quanto rende le funzioni seno e coseno strumenti universali per descrivere rotazioni e periodicità.
Proprietà fondamentali e periodicità
Come abbiamo accennato poco fa, seno e coseno posseggono alcune specifiche proprietà che li rendono essenziali nell’ambito della matematica e della fisica.
In particolare, una caratteristica chiave è la loro periodicità: entrambe le funzioni si ripetono con un periodo di 2π radianti, cioè ogni volta che l’angolo aumenta di 360°, i valori di seno e coseno tornano a quelli iniziali. Questo comportamento:
- riflette fenomeni ciclici, come ad esempio il movimento di un pendolo o le onde sonore;
- permette di modellare situazioni che si ripetono nel tempo o nello spazio;
- facilita l’analisi e la risoluzione di problemi.
Ad esempio, dato il seno di 30°, che è 0,5, lo stesso valore si ritroverà al seno di 390° (ossia 30° + 360°), confermando la periodicità. Inoltre, seno e coseno sono funzioni limitate, che assumono valori compresi tra -1 e 1, il che significa che non crescono all’infinito ma oscillano sempre entro questi limiti.
Un’altra proprietà importante è la simmetria: il coseno è una funzione pari, cioè cos(−x) = cos(x), mentre il seno è una funzione dispari, quindi sen(−x) = −sen(x). Queste simmetrie si riflettono anche nel grafico delle due funzioni, dove il coseno appare come una curva simmetrica rispetto all’asse verticale, mentre il seno è simmetrico rispetto all’origine.
Relazioni e formule fondamentali
Seno e coseno sono collegati da una serie di formule e relazioni che ne permettono l’uso versatile in moltissimi ambiti.
Tra queste è di certo necessario menzionare:
- relazione pitagorica. Nello specifico essa lega i quadrati di seno e coseno di uno stesso angolo e stabilisce che la loro somma è sempre uguale a 1: sen²(θ) + cos²(θ) = 1. Ad esempio, dato un angolo di 45°, il seno e il coseno valgono entrambi circa 0,707 ed elevati al quadrato e sommati danno in risultato 1 (0,707² + 0,707² ≈ 1);
- formule di addizione e sottrazione: permettono di calcolare il seno e il coseno di somme o differenze di angoli: sen(α + β) = sen α cos β + cos α sen β, e cos(α + β) = cos α cos β − sen α sen β. Ad esempio, dati seno e coseno di 30° e 60°, è possibile calcolare il seno di 90° (30° + 60°) che equivale a 1;
- scomposizione di vettori in componenti ortogonali: ciò avviene grazie alla loro capacità di rappresentare proiezioni sull’asse orizzontale e verticale. Se un vettore ha intensità 10 e forma un angolo di 60° con l’asse x, la componente orizzontale è 10 × cos 60° = 5, mentre quella verticale è 10 × sen 60° ≈ 8,66.
Seno e coseno come linguaggio universale
Le funzioni seno e coseno sono molto più che semplici concetti geometrici. Posseggono infatti una grande importanza in molti campi e rappresentano un linguaggio universale che attraversa molte discipline. Grazie alla loro periodicità e semplicità di manipolazione, infatti, permettono di rappresentare con precisione qualsiasi fenomeno periodico e di decomporlo in componenti elementari.
Nello specifico:
- matematica: sono la base per la definizione delle funzioni trigonometriche inverse, per la risoluzione di equazioni, e per l’analisi dei segnali;
- fisica: descrivono fenomeni oscillatori come il moto armonico semplice, le onde elettromagnetiche e le vibrazioni meccaniche. Ad esempio, il moto di una molla che si allunga e si contrae periodicamente può essere modellato con una funzione seno, dove il tempo è la variabile e la posizione della molla è proporzionale al valore del seno di quell’istante;
- ingegneria: permettono l’analisi delle strutture, la progettazione di circuiti elettrici e lo studio delle onde sonore.
Come abbiamo analizzato insieme seno e coseno sono due elementi estremamente importanti in quanto rendono la comprensione di molte nozioni di matematica, fisica, ingegneria ed altre scienze applicate. In definitiva, non sono solo semplici funzioni ma la chiave per comprendere il mondo ciclico che ci circonda.