Calcolare il volume del cilindro
Ci sono numerose situazioni, nella nostra vita di tutti i giorni, in cui potremmo trovarci a dover calcolare il volume cilindro. Questo calcolo, solo per fare un esempio, è necessario quando ci troviamo a dover gestire fluidi, che si tratti di gas o liquidi. Calcolare il volume di un contenitore cilindrico può rivelarsi necessario per riempirlo con il fluido di nostro interesse.
Per chi progetta sistemi atti a gestire i fluidi, quindi, conoscere la formula corretta è fondamentale. Il volume esatto di un contenitore cilindrico permette di gestire un fluido in maniera corretta in ogni situazione.
Se si lavora con sistemi idraulici, nei quali anche la portata e la pressione di un fluido sono essenziali, il calcolo corretto è ancora più importante. È vero che oggi esistono calcolatori automatici, anche online, che ci permettono di stabilire il volume di un cilindro semplicemente inserendone i dati.
Tuttavia, in alcune situazioni potrebbe essere necessario effettuare un calcolo senza l’ausilio di strumenti informatizzati. Ecco perché, in questa guida, scopriremo tutto sulla formula, la definizione di volume e le applicazioni reali.
Volume cilindro: perché è importante
Abbiamo già anticipato che il calcolo corretto del volume cilindro è fondamentale in molti campi. In primis, per progettare e ottimizzare sistemi adeguati alla gestione dei fluidi.
E non ci riferiamo solamente alle situazioni per cui un gas o un liquido devono essere semplicemente conservati in un contenitore. Quando un cilindro è inserito in un sistema, per esempio in una pompa, è di basilare importanza che il volume del cilindro venga calcolato accuratamente.
I sistemi di stoccaggio di gas e liquidi, ma anche i sistemi idraulici, sono solo due degli esempi in cui il calcolo corretto è necessario.
Anche quando i fluidi devono essere conservati, come nel caso delle operazioni di stoccaggio, è fondamentale che il calcolo del volume dei contenitori sia accuratissimo.
Questo per evitare che il fluido fuoriesca o che, al contrario, il contenitore non venga riempito al massimo.
Le conseguenze di un errore
Un errore nel calcolo del volume cilindro, in alcune circostanze, potrebbe avere implicazioni anche gravi. In base alle caratteristiche dei fluidi da conservare, per esempio, si potrebbe incorrere in problemi legati alla sicurezza.
Se, invece, il livello del fluido stoccato è insufficiente, si potrebbero generare problemi di mancata efficienza.
E, se inserito in contesto di un sistema, per esempio idraulico, il rischio è quello di danneggiare le diverse componenti o, nei casi più gravi, l’intero sistema.
Nei casi meno gravi, un errore di calcolo può comportare una mancanza di efficienza che, anche se lieve, potrebbe generare problemi legati allo spreco di risorse. Di conseguenza, non sono escluse perdite economiche. Un sistema non efficiente, infatti, non solo consuma di più in termini di energia, ma può anche essere causa di spreco di risorse e materiali.
Volume cilindro: definizione e formule
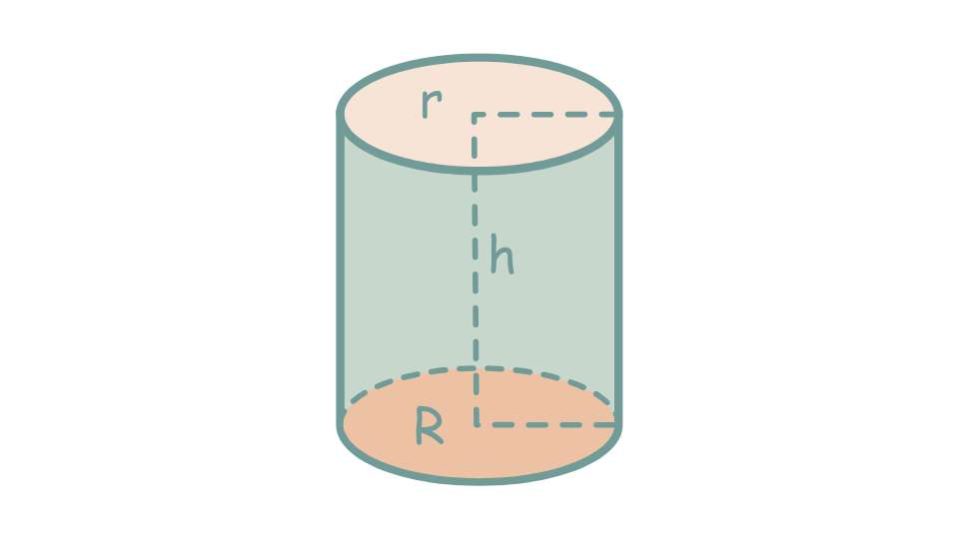
Il volume cilindro non è altro che la misura dello spazio tridimensionale occupato da questo solido geometrico. Detto in parole più semplici, possiamo indicarlo come la quantità di spazio che il cilindro racchiude al suo interno.
Per il suo calcolo, basta moltiplicare l’area della base per l’altezza del cilindro. Dato che la base di un cilindro è un cerchio, l’area di base si calcola con la formula seguente:
Area di base = π × r²
Nella formula, r rappresenta il raggio del cerchio di base.
Di conseguenza, la formula completa per il volume del cilindro è questa:
V = π × r² × h
Nella formula, ovviamente, h sta per l’altezza del cilindro stesso, mentre V è il volume da calcolare.
Quando si ha l’area di base già a disposizione, invece, la formula da usare è la seguente:
V = Abase x h
Abase, in questo caso, indica l’area di base.
Le formule inverse
Dalla formula di base del volume cilindro è possibile ricavare le cosiddette formule inverse.
Se, per esempio, è necessario calcolare l’altezza, avendo a disposizione il volume e l’area di base la formula da usare è questa:
h = V/Abase
Al contrario, se ci serve l’area di base e abbiamo a disposizione i dati su volume e altezza, useremo questa formula inversa:
Abase = V/h
In alcuni casi, potrebbe essere necessario calcolare la misura del raggio della base. La formula per il calcolo del raggio è lievemente più complessa. Tuttavia, avendo a disposizione volume e altezza, il calcolo è possibile con questa formula:
r = √[V/(π ∙ h)]
In alternativa, a seconda dei dati a disposizione, possiamo usare le seguenti formule per calcolare il raggio di base:
- r = √(Ab/π) se disponiamo dell’area del cerchio di base
- r = Slat/(2π ∙ h) se, invece, abbiamo il dato relativo alla superficie laterale
Queste sono invece le formule inverse per trovare l’area del cerchio di base, a seconda dei dati disponibili:
- con il volume, Ab = V/h
- con la superficie, Ab = (Stot – Slat)/2
- con il raggio, Ab = πr2
Per trovare la superficie totale, la formula base è la seguente:
Stot = Slat + 2Ab
Possiamo trovare la superficie totale anche se non abbiamo a disposizione la superficie laterale e l’area di base, utilizzando i seguenti dati:
- con raggio e altezza, Stot = (2πr ∙ h) + 2πr2 = 2πr(r + h)
Queste, invece, sono le formule per calcolare la superficie laterale:
- Slat = Stot – 2Ab
- con raggio e altezza, Slat = 2πr ∙ h
Circonferenza e altezza
Dalla formula del volume cilindro si possono infine ricavare anche altri dati relativi a questo solido.
Partendo dall’altezza, se si hanno a disposizione volume e area di base, come abbiamo già detto, la formula da usare è h = V/Abase.
Tuttavia, esistono altre due modalità per calcolare l’altezza:
- h = Slat/(2πr) utilizzando quindi la superficie laterale
- h = V/πr2 sfruttando il volume
Se, infine, è necessario calcolare la circonferenza del cerchio di base, la formula da usare è questa:
Cb = 2πr