La legge di Biot-Savart e il filo elettrico
Attribuita ai fisici francesi Jean-Baptiste Biot e Félix Savart, permette di calcolare il campo magnetico prodotto da un filo percorso da corrente elettrica. Per la precisione si parla di una legge riferita a un filo rettilineo indefinito. In pratica questo può avere qualsiasi lunghezza ma il principio varrà comunque.
La si considera non a caso una delle equazioni fondamentali per studiare l’elettromagnetismo, e permette di determinare il campo magnetico in un qualsiasi punto dello spazio. In più aiuta a spiegare la relazione fra il magnetismo e le correnti elettriche.
La relazione con l’esperimento di Ørsted
Prima della definizione della legge di Biot-Savart un fisico danese di nome Hans Christian Ørsted aveva già scoperto la correlazione fra elettricità e magnetismo. Si trattò cronologicamente della prima dimostrazione empirica di come una corrente generasse un campo magnetico, sfruttando l’ago magnetico di una bussola. Non fu un esperimento ufficiale, ma più un evento casuale mentre Ørsted preparava il materiale per una lezione di Fisica.
Il fisico notò infatti che avvicinando una bussola a un filo percorso da corrente l’ago iniziava a muoversi senza più segnare i poli correttamente. Provò allora a condurre esperimenti più approfonditi e scoprì che sopra una certa intensità la corrente riusciva a orientare l’ago in modo che risultasse perpendicolare alla disposizione del cavo. Da qui riuscì a dedurre che l’elettricità creasse un campo magnetico in grado di influenzare l’ago. Infatti nel momento in cui il flusso della corrente si interrompeva la bussola riprendeva a funzionare correttamente.
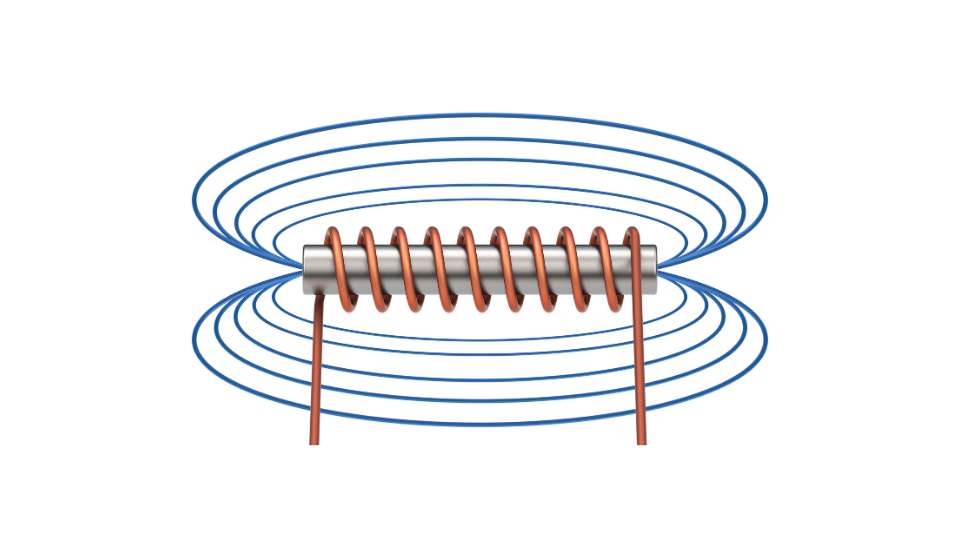
L’esperimento di Ørsted risale al 1811, ma la legge di Biot-Savart che definiva come calcolare il modulo del campo magnetico B arrivò solo nove anni dopo. Il fisico danese però riuscì anche a capire la disposizione delle linee di campo con un secondo esperimento molto semplice. Sparse della limatura di ferro attorno al filo elettrificato, che essendo un materiale in grado di magnetizzarsi si dispose subito secondo le linee del campo B. Ogni piccola scheggia di limatura si comporta infatti come un minuscolo ago magnetico. Le linee così descritte risultarono circolari e concentriche rispetto al cavo.
Calcolare il campo magnetico con la legge di Biot-Savart
I due fisici francesi che le danno il nome svolsero diversi studi per arrivare alla formula che vedremo. Per introdurla possiamo dire che il campo magnetico B risulta direttamente proporzionale alla corrente che scorre all’interno del filo elettrificato. Poiché si può usare per qualsiasi punto dello spazio intorno al filo bisogna precisare anche che B è inversamente proporzionale alla distanza fra il punto considerato e il filo.
La formula definita dalle legge di Biot-Savart perciò è B = μ0i/2πd.
Analizzandola precisiamo che:
- μ0 rappresenta la costante di permeabilità magnetica nel vuoto e fa parte delle costanti fisiche fondamentali. il suo valore è fissato a 4π x 10-7 Tm/A (T = Tesla e A = Ampère). Il Tesla misura il campo magnetico e l’Ampère la corrente elettrica.
- i è la corrente che passa nel filo.
- d è la distanza tra il punto in cui si sta misurando il campo magnetico e il filo elettrico.
Più si è distanti dal filo minore sarà l’intensità del campo magnetico, mentre più aumenta la corrente più il valore di B salirà a sua volta. A una distanza infinita dal filo il campo sarà nullo per convenzione. Se rappresentassimo la distanza e il campo magnetico in un grafico mettendo la prima sulle ascisse e il secondo sulle ordinate otterremmo il ramo di un’iperbole equilatera che tende a zero all’aumentare della distanza.
Per determinare la distanza a cui ci troviamo dal filo conoscendo il valore del campo magnetico possiamo usare la formula inversa d = μ0i/2πB. Se invece conosciamo sia d che B ma non l’intensità della corrente la formula inversa da usare i = 2dπB/μ0.
Un esempio pratico
Prima di tutto vediamo che il testo del problema fornisce già i valori della corrente e della distanza fra il filo e il punto di interesse. Tuttavia d deve essere espressa in metri, dunque dovremo convertire la misura di 25 cm scrivendo 0,25 m. Anche per la corrente occorre una conversione dato che 70 mA corrispondono a 0,007 Ampère (A). Solo a questo punto abbiamo tutti i valori necessari per procedere al calcolo di B nel punto P.
Usando la formula vista prima quindi scriveremo che B = 4π x 10-7 x 0,007/2π x 0,25. Possiamo semplificare il valore π visto che è presente sia al numeratore che al denominatore, e il risultato che otteniamo è 2,24 x 10-8 T.
Le applicazioni pratiche della legge di Biot-Savart
Lo stesso vale nella costruzione delle linee elettriche di trasmissione, che hanno lo scopo di portare la corrente a grandi distanze dalla centrale di produzione. In questo caso questo principio permette di determinare l’interazione fra il flusso delle corrente e i campi magnetici che può incontrare.
Grazie alla legge di Biot-Savart quindi è possibile ridurre al minimo le perdite lungo i cavi e rendere perciò più efficienti le linee di trasmissione. Anche nella progettazione dei circuiti elettrici e dei cablaggi la legge di Biot-Savart si rivela utile. Consente infatti di capire se si vengano a creare campi magnetici che possano interferire con il funzionamento di alcune delle componenti.
In questo modo è possibile apportare le opportune modifiche per far sì che il circuito o il cablaggio permettano un corretto flusso della corrente.